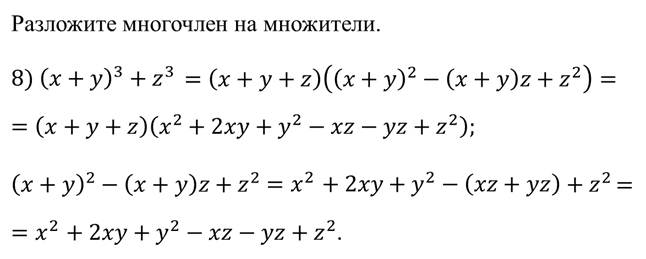Вопросы занятия:
· повторить все известные нам способы разложения многочленов на множители;
· рассмотреть разложение многочленов на множители, применяя последовательно несколько способов.
Материал урока
На предыдущих уроках мы познакомились с различными способами разложения многочленов на множители.
Напомним, что разложение многочлена на множители – это представление многочлена в виде произведения двух или нескольких многочленов.
Первый способ, который мы рассмотрели, – это вынесение общего множителя за скобки. Вспомним его.
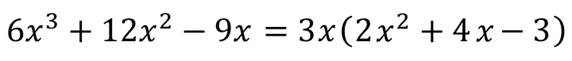
Затем мы познакомились со способом группировки.
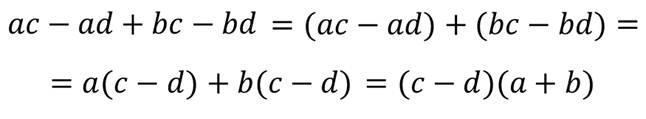
Далее мы познакомились с разложением на множители с помощью формул сокращённого умножения, а именно, с помощью формул квадрата суммы
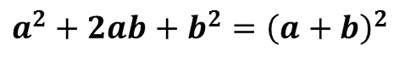
и квадрата разности,
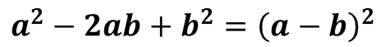
с помощью формулы разности квадратов,
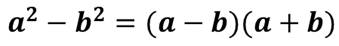
с помощью формул куба сумм
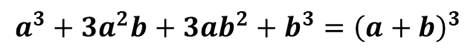
и куба разности,
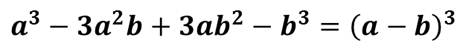
а также с помощью формул суммы кубов
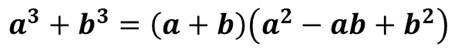
и разности кубов
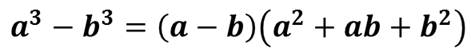
Однако чаще всего каждый из этих способов в отдельности не приводит к цели, поэтому для разложения многочлена на множители приходится пользоваться их комбинацией.
Давайте рассмотрим примеры.
Пример.
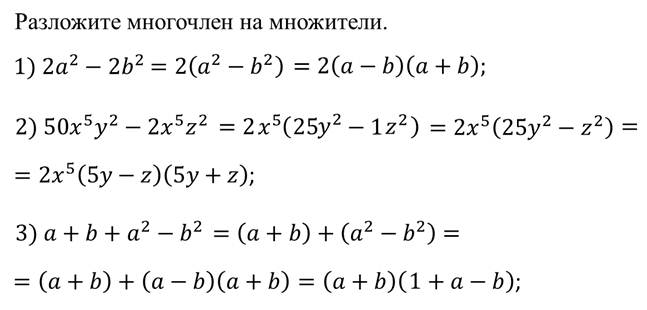
Пример.

Пример.
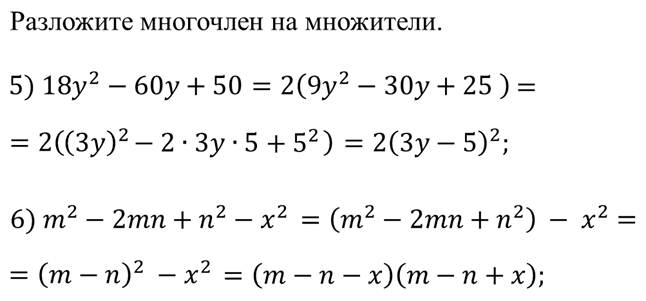
Пример.
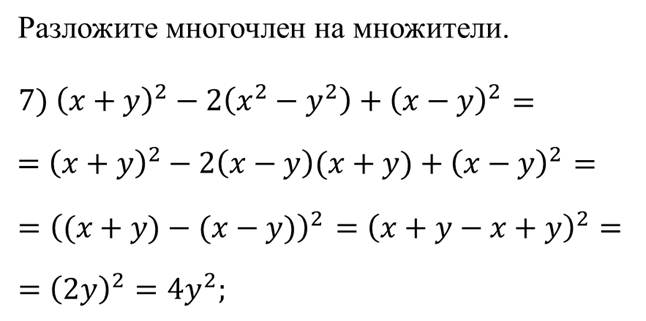
Пример.