Давайте вспомним, что по величине углов выделяют остроугольные, прямоугольные и тупоугольные треугольники. А также отметим, что сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами.
Сумма углов любого треугольника равна 180 градусов.
Теорема:
В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона.
Доказательство:
1. Докажем, что против большей стороны лежит больший угол.
Возьмём некоторый треугольник АВС. Пусть АВ>ВС. Отложим сторону ВС на стороне АВ, то есть отрезок ВЕ=ВС.
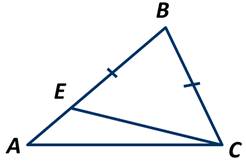
Так как получается, что треугольник ЕВС — равнобедренный, то углы при основании равны.
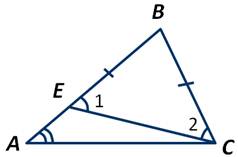
В треугольнике АЕС ∠А<∠1, так как внешний угол больше любого внутреннего, не смежного с ним. В треугольнике АВС ∠С>∠2.
Получаем:
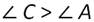
То есть, против большей стороны АВ лежит больший ∠С. Что и требовалось доказать.
2. Докажем, что против большего угла лежит большая сторона.
Пусть ∠С>∠А треугольника АВС.
Предположим, что АВ<ВС, то по доказанной первой части данной теоремы ∠С<∠А. Получили противоречие.
Если АВ=ВС, то получается, что треугольник АВС равнобедренный, а тогда ∠С=∠А. Снова противоречие.
Так как в каждом из предыдущих случаев наше предположение неверно, тогда получаем, что АВ>ВС. Теорема доказана.
Следствие:
В прямоугольном треугольнике АВС гипотенуза АВ больше катетов АС и ВС. Действительно, верно, так как гипотенуза лежит против прямого угла, а катеты — против острых, градусная мера которых меньше 90 градусов.
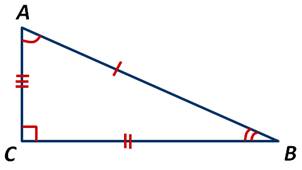
Признак равнобедренного треугольника:
Если два угла треугольника равны, то треугольник равнобедренный.
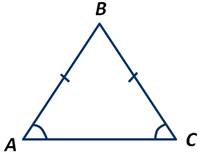
Доказательство:
Пусть АВС треугольник, у которого углы А и С равны. Докажем, что равны стороны АВ и ВС, лежащие против этих углов.
Предположим, что АВ>ВС. Тогда по предыдущей теореме ∠С, лежащий против большей стороны АВ, будет больше ∠А, лежащего против меньшей стороны ВС. Получили противоречие условию равенства углов А и С.
Предположение неверно и стороны АВ и ВС равны, то есть треугольник АВС является равнобедренным. Что и требовалось доказать.
Пример.
В треугольнике АВС сторона АВ=9 см, а сторона ВС=14 см. Какой из углов является большим — А или С?
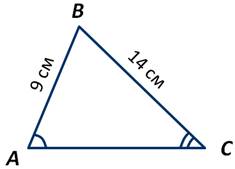
По теореме о соотношениях между сторонами и углами треугольника против большей стороны лежит больший угол. Следовательно, получаем:
Так как ∠A лежит против большей стороны ВС.
Пример.
В треугольнике АВС ∠А=45 градусов, а ∠В=65 градусов. Верно ли, что сторона АС больше каждой из сторон АВ и ВС?
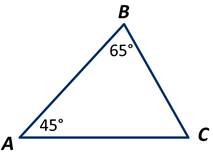
По теореме о сумме углов треугольника, получаем:
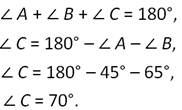
Воспользовавшись теоремой о соотношениях между сторонами и углами треугольника, выяснили, так как против большего угла лежит большая сторона, а в нашем случае большую градусную меру имеет ∠С, то большей стороной треугольника является сторона АВ.
Ответ: неверно, что сторона АС больше каждой из сторон АВ и ВС
Теорема о соотношении между сторонами и углами треугольника
Теорема: В треугольнике
1. Против большей стороны лежит больший угол
2. Обратно, против большего угла лежит большая сторона.
1. Дано: АВ>АС
Доказать: ∠С>∠В.
Доказательство: Отложим отрезок AD равный отрезку АС и тогда точка D будет лежать между точек А и В. Луч CD рассечёт угол АСВ на два угла, при этом ∠1=∠2. ΔАСВ состоит из углов ∠1 и ∠3. ∠2 – внешний для треугольника CDB, значит он больше угла В.

Рис. 1. Теорема о соотношении между сторонами и углами треугольника
AD=AC<AB
∠1=∠2<∠ACB
∠2=∠B+∠3>∠B
∠1>∠B
∠ACB>∠B, что и требовалось доказать.
2. Дано: ∠С>∠В
Доказать: ∠АВ>∠AC
Доказательство: Докажем методом от противного.

Рис. 2. Обратная теорема о соотношении между сторонами и углами треугольника ![]() , но ∠С>∠В по условию, следовательно, остается только случай, если АВ>АС, что и требовалось доказать.
, но ∠С>∠В по условию, следовательно, остается только случай, если АВ>АС, что и требовалось доказать.
Ещё раз сформулируем теорему и распространим её на все углы треугольника.
Теорема: В треугольнике
1. Против большей стороны лежит больший угол
2. Обратно, против большего угла лежит большая сторона.

Рис. 3. Чертёж к теореме
Если АВ>AC>BC, то ∠C>∠B>∠A.
Если ∠C>∠B>∠A, то АВ>AC>BC.
Следствие 1 из теоремы
Следствие 1: В прямоугольном треугольнике гипотенуза больше катета.
Доказательство:

Рис. 4. Чертёж к следствию 1
∠А+∠В+90=180, ∠А+∠В=90=∠С. Отсюда следует, что ∠А<90, ∠В<90. Значит, СВ<АВ, СА<АВ. Гипотенуза АВ больше одного катета и больше другого катета. Следствие доказано.
Следствие 2 из теоремы
Следствие 2: Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Дано: ∠В=∠С
Доказать: АС=АВ
Доказательство: Докажем методом от противного.

Рис. 5. Чертёж к следствию 2
АВ>АС ∠С>∠В, то есть АВ=АС. Следствие доказано.
Обсудим следствие 2. Треугольник называется равнобедренным, если его две стороны равны. Из этого вытекает его свойство: углы при основании равны. А теперь у нас есть признак, что если углы при какой-либо стороне равны, то треугольник равнобедренный. Мы имеем признак равнобедренного треугольника.
Решение задач
Пример 1: Сравните углы треугольника и выясните, может ли быть угол А тупым, если АВ=АС<ВС.

Рис. 6. Чертёж к примеру 1
АВ=АС ∠С=∠В. АС<ВС ÐВ<ÐА. Мы получили соотношение между углами: ∠С=∠В ∠А=180-(∠В+∠С).
Пример: ∠В=∠С=10, тогда ∠А=180-(10+10)=160.
Ответ: 1) ∠В=∠С<∠А 2) ∠А может быть тупым.
На сегодняшнем уроке мы рассмотрели теорему об отношении между сторонами и углами треугольника. На следующем уроке мы рассмотрим тему о неравенстве треугольников.