Прямая. Луч. Отрезок. Ломаная. Многоугольник
Прямая
Прямая бесконечна (в обе стороны) и разбивает плоскость на две полуплоскости, для которых прямая является границей. Граница принадлежит полуплоскостям.
На рисунке точка С лежит на прямой между точками А и В, которые лежат по разные стороны от точки С. Точки С и В лежат по одну сторону от точки А. Из трех точек на прямой одна и только одна точка лежит между двумя другими.
Аксиома прямой. Через любые две точки плоскости можно провести прямую, и притом только одну.
Две прямые называются пересекающимися, если они имеют общую точку.
Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Если прямые а и b параллельны, то отрезки, изображающие эти прямые, никогда не пересекутся, сколько бы их ни продолжали.
Луч
Лучом называется часть прямой, ограниченная одной точкой.
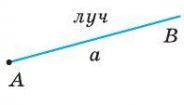
Точка, ограничивающая луч, принадлежит лучу и называется началом луча. Луч бесконечен (в одну сторону). Он обозначается одной малой буквой, или двумя большими буквами, где первой всегда записывается начало луча. При этом вторая точка может быть не отмечена на луче. Она указывает направление луча, например как точка В на луче АВ.
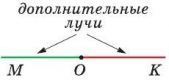
Два луча называются дополнительными (противоположными), если они имеют общее начало и лежат на одной прямой.
На рисунке изображены дополнительные лучи ОМ и ОK. Они дополняют друг друга до прямой.
Чтобы построить луч, дополнительный данному, достаточно продлить данный луч за его начало вдоль прямой, на которой лежит данный луч. Любая точка прямой разбивает ее на два дополнительных луча.
Отрезок
Отрезком называется часть прямой, ограниченная двумя точками.
Точки, ограничивающие отрезок, принадлежат отрезку и называются концами отрезка, остальные точки отрезка — его внутренними точками. На рисунке изображен отрезок АВ с концами А и В. Точка М — внутренняя точка отрезка АВ.
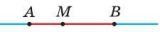
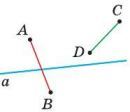
Если концы отрезка лежат в разных полуплоскостях относительно прямой, то этот отрезок пересекает прямую, если в одной полуплоскости — то не пересекает. На рисунке концы отрезка АВ лежат в разных полуплоскостях относительно прямой а, и он пересекает прямую а. Концы же отрезка CD лежат в одной полуплоскости, и он не пересекает прямую а.
Два отрезка называются равными, если их можно совместить наложением.
Важной характеристикой отрезка является его длина.
Свойства длины отрезка: каждый отрезок имеет длину, выраженную положительным числом; равным отрезкам соответствуют равные длины, большему отрезку — большая длина. И наоборот.
Аксиома измерения отрезков. Если на отрезке взять точку, то она разобьет данный отрезок на два отрезка, сумма длин которых равна длине данного отрезка.
Аксиома откладывания отрезков. На любом луче от его вершины можно отложить отрезок данной длины, и притом только один.
На рисунке точка С лежит на отрезке АВ. По аксиоме измерения отрезков следует, что АС + СВ = АВ.
Серединой отрезка называется точка, которая делит отрезок на два равных отрезка. На рисунке точка М — середина отрезка EF, то есть EM = MF.
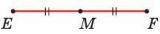
Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки.
На рисунке расстояние между точками K и N равно длине отрезка KN.
Ломаная
Ломаной называется геометрическая фигура, образованная отрезками, последовательно соединенными своими концами, у которой никакие два соседних звена не лежат на одной прямой. Длиной ломаной называется сумма длин ее звеньев.
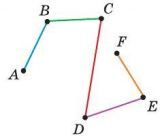
На рисунке изображена ломаная ABCDEF. Указанные отрезки называются звеньями ломаной, а точки A, B, C, D, E и F — вершинами ломаной.
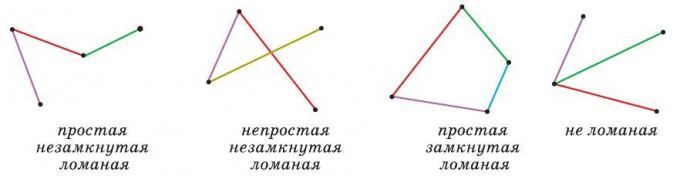
Ломаная называется замкнутой, если начало ее первого звена совпадает с концом последнего. В противном случае она называется незамкнутой. Ломаная называется простой, если она не имеет самопересечений и никакие два ее звена, кроме соседних, не имеют общих точек. В противном случае она называется непростой.
Многоугольник
Мы уже говорили о возможных вариантах взаимного расположения трех прямых на плоскости: все три параллельны, все три пересекаются в одной точке, две параллельные, а третья их пересекает. Но все это предельные случаи, которые мы либо уже рассмотрели, либо будем их изучать в дальнейшем.
Но если бросить на стол три спички и продлить каждую из них до прямой, то получится три попарно пересекающиеся прямые (см. рис. 1). Можно сказать, что вероятность этого события равна 
или что все оставшиеся варианты расположения трех прямых на плоскости столь же вероятны, как и выпадение монеты на ребро.
Рис. 1. Три попарно пересекающиеся прямые
Попарное пересечение трех прямых образует фигуру, которую мы и будем сейчас изучать – треугольник (см. рис. 2).
Рис. 2. Попарное пересечение трех прямых образует треугольник
Самая простая «конечная» фигура – отрезок. Что можно нарисовать из отрезков? Если рисовать отрезки так, чтобы конец одного был началом другого, то получится фигура, которая называется ломаной (см. рис. 3) (в каждой узловой точке как бы ломается), а отрезки, из которых она состоит, называются звеньями.
Рис. 3. Пример ломаной
Сами по себе ломаные – полезные фигуры, поскольку они позволяют приближать различные кривые, а значит, помогают вычислять их длину (см. рис. 4).
Рис. 4. Приближение кривой ломаной
Но особый интерес представляют собой замкнутые ломаные – т. е. те, которые являются границами какой-то области на плоскости (см. рис. 5).
Рис. 5. Замкнутая ломаная
Замкнутую ломаную без самопересечений называют многоугольником (фигура, у которой много углов) (см. рис. 6).
Рис. 6. Пример многоугольника
Из двух отрезков замкнутую ломаную не нарисуешь, значит, наименьшая возможная замкнутая ломаная состоит из 
звеньев. Или, по-другому, наименьший из возможных многоугольников – треугольник (см. рис. 7).
Рис. 7. Треугольник – наименьший из возможных многоугольников
Почему многоугольникам и, в частности, треугольникам уделяют так много внимания в геометрии? Любую сложную фигуру можно приблизить как угодно точно многоугольниками. Поэтому, изучая свойства многоугольников, мы можем работать с фигурами любой формы.
Но любой многоугольник можно разбить на треугольники. Это облегчает изучение многих свойств различных многоугольников и сводит их к изучению свойств одной фигуры – треугольника.
