Угол. Виды углов
Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Два угла называются равными, если их можно совместить наложением.
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
На рисунке луч AK — биссектриса угла BAC и ∠BAK = ∠CAK.
Развернутым углом называется угол, стороны которого являются дополнительными лучами.
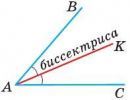
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
На рисунке луч AK — биссектриса угла BAC и ∠BAK = ∠CAK.
Развернутым углом называется угол, стороны которого являются дополнительными лучами.
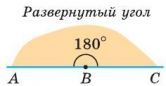
На рисунке угол ABC — развернутый, лучи BA и BC — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой AC также задает развернутый угол ABC.
Углы измеряются в градусах, минутах, секундах.
Развернутый угол равен 180°; 1/180 часть развернутого угла называется градусом и обозначается 1°; 1/60 часть одного градуса называется минутой и обозначается 1′; 1/60 часть минуты называется секундой и обозначается 1″.
Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).
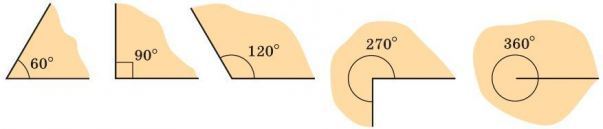
На рисунке последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.
Свойства градусной меры угла:
· любой угол имеет градусную меру, выраженную некоторым положительным числом;
· равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.
Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.
Задача.
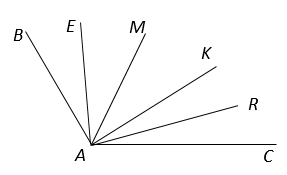
Дано: ∠ВАС = 120°, ∠MAR =40°, луч АЕ — биссектриса ∠ВАМ, луч AR — биссектриса ∠САК.
Найти: ∠ЕАR.
Смежные углы. Вертикальные углы
Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
Если на рисунке лучи ОА и ОВ дополнительные, то углы АОС и ВОС — смежные.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.

Следствия.
1. Если смежные углы равны, то каждый из них прямой.
2. Если два угла равны, то равны и смежные с ними углы.
Задача 1. Один из смежных углов в 3 раза больше другого. Найдите эти углы.
Задача 2. Один из смежных углов в 2 раза больше другого. Найдите эти углы.
Задача 3. Один из смежных углов на 20° больше другого. Найдите эти углы.
Задача 4. На рисунке лучи ОК и ОМ — дополнительные, угол MON на 70° больше угла NOK. Найдите ∠ MON.
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.
При пересечении двух прямых AC и DB в точке O получим, что лучи OA и OC, OB и OD — дополнительные. Поэтому углы AOD и BOC — вертикальные. Углы AOB и DOC также вертикальные.

Теорема (свойство вертикальных углов). Вертикальные углы равны.
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов.
Угол между параллельными прямыми считается равным 0°.
Задача 6. На рисунке ∠ВОС = 1/3∠АОС, ∠NOC = 90°. Найдите ∠АОК.