Мы начинаем изучать новый предмет — геометрию.
В переводе с греческого слово «геометрия» означает «землемерие» (гео — земля, метрео — мерить). Это одна из самых древних наук.
Зарождение геометрии было связано с необходимостью определять размеры участков земли, ориентироваться по расположению звёзд на небе, строить здания и сооружения. В результате такой деятельности накопилось много правил, связанных с геометрическими построениями и измерениями, и геометрия сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.

На уроках математики вы познакомились с такими геометрическими фигурами как:
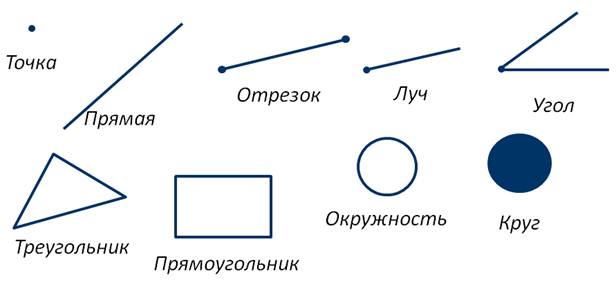
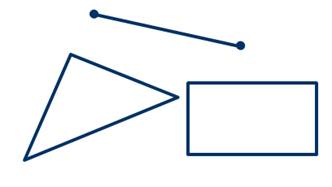
Школьный курс геометрии делится на планиметрию и стереометрию. В планиметрии рассматриваются свойства уже известных вам фигур на плоскости, таких, как отрезок, прямоугольник, треугольник:
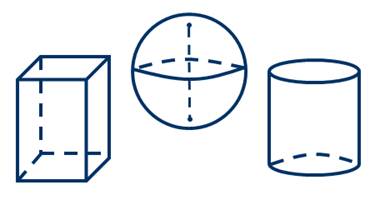
В стереометрии изучаются свойства фигур в пространстве. Примерами таких фигур являются параллелепипед, шар, цилиндр:
Мы начнём изучение геометрии с планиметрии.
Давайте поговорим о точках, прямых и отрезках. Точки обозначаются большими латинскими буквами:

Прямые обычно обозначаются малыми латинскими буквами. Прямая не имеет толщины и ширины, простирается неограниченно в обе стороны. Туго натянутая нить даёт нам представление о прямой:

Часть прямой а, ограниченная двумя точками А и В (Б), называется отрезком. Точки А и В, ограничивающие отрезок, называются концами отрезка. Такой отрезок обозначается АВ или ВА.

Поговорим о свойствах прямой. Возьмём некоторую прямую а, точки А и В, которые лежат на прямой а, и точки C и D, которые не лежат на этой прямой. Другими словами можно сказать, что прямая проходит через точки А и В, но не проходит через точки C и D. Отметим, что через точки А и В нельзя провести другую прямую, которая не совпадала бы с прямой а:
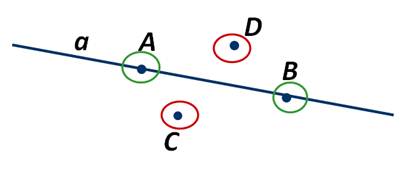
Таким образом, можно сформулировать следующее свойство:
Через любые две точки можно провести прямую и притом только одну.
Рассмотрим теперь две прямые. Если прямые а и b имеют одну общую точку О, то говорят, что они пересекаются в этой точке. А вот прямые p и q не пересекаются:
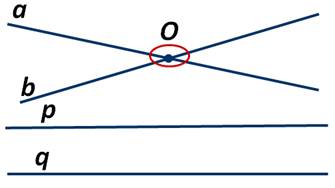
Любые две прямые могут иметь не более одной общей точки. Так как иначе, исходя из сформулированного выше свойства, они будут совпадать. Таким образом, можно сделать вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Домашнее задание
Страница: 5 — 7 читать
Упражнения №1 — №7