Первый признак равенства треугольников:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
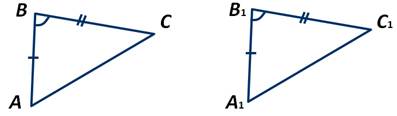
Второй признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
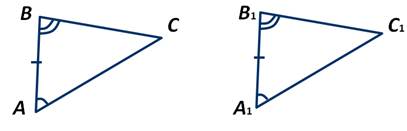
Доказательство:
Пусть АВС и А1В1С1 — треугольники, у которых АВ=А1В1, ∠А=∠А1, ∠В=∠В1. Доказать, что ∆ АВС= ∆ А1В1С1.
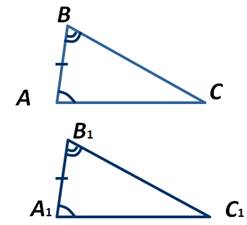
Наложим треугольник АВС на треугольник А1В1С1 таким образом, чтобы вершина А совместилась с вершиной А1, сторона АВ — с равной ей стороной А1В1, а вершины С и С1 оказались по одну сторону от прямой А1В1.
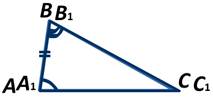
Так как ∠А=∠А1 и ∠В=∠В1, то сторона АС наложится на луч А1С1, а сторона ВС — на луч В1С1. Поэтому вершина С (общая точка сторон АС и ВС) окажется лежащей на лучах А1С1 и В1С1, а следовательно, совместится с общей точкой этих лучей — вершиной С1. Значит, совместятся стороны АС и А1С1, ВС и В1С1. Получаем, что ∆ АВС и ∆ А1В1С1 полностью совместятся, то есть они равны.
Пример.
Доказать, что в равнобедренном треугольнике биссектрисы, поведённые к боковым сторонам, равны между собой.
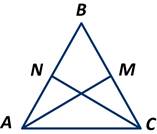
Пусть треугольник АВС равнобедренный, у которого АВ=ВС. АМ и CN — биссектрисы. Рассмотрим треугольники АМВ и CNB. У них угол В — общий, АВ=ВС по условию, углы NСВ и МАВ равны как половинки двух равных углов при основании равнобедренного треугольника.
Тогда получаем, что ∆ АМВ=∆ CNB по второму признаку. Откуда следует, что АМ=СN.
Пример.
Точки Е и F лежат соответственно на сторонах АВ и CD квадрата ABCD так, что ∠FВС=∠ЕDА. Доказать, что ∆ СBF= ∆ ADE.
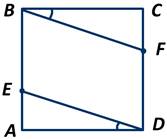
Рассмотрим ∆ СBF и ∆ ADE. У них сторона ВС=AD, так как все стороны квадрата равны, ∠ВСF=∠DAE, так как все углы квадрата прямые, ∠FВС=∠ЕDА по условию задачи. А следовательно, ∆ СBF и ∆ ADE равны по второму признаку равенства треугольников.
Пример.
Отрезки АВ и CD пересекаются в точке Е, которая является серединой отрезка АВ, а ∠EAD и ∠EBC — равны. Доказать, что ∆ СВЕ и ∆ ADE равны. Чему равна длина отрезка AD, если отрезок СВ=7 см?
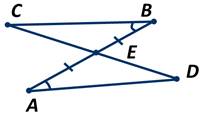
Рассмотрим ∆ СВЕ и ∆ ADE. У них сторона АЕ=ВЕ, так как Е — середина отрезка АВ. ∠EAD и ∠EBC равны по условию задачи. А ∠СЕВ и ∠AED равны как вертикальные. Получаем, что ∆ СВЕ и ∆ ADE равны по второму признаку. Следовательно, у них соответственные стороны равны. Значит, сторона AD=СВ. То есть AD=7 см.
Примеры решения задач
Пример 1: По данным рисунка докажите, что АО = ОС, АВ = CD, ∠А = ∠С.
Дано: ВО = ОD, ∠В = ∠D.
Доказать: АО = ОС, АВ = CD, ∠А = ∠С.

Рис. 3. Чертеж к примеру 1
Доказательство:

Из равенства треугольников следует равенство их соответствующих элементов, а именно, что АО = ОС, АВ = CD, ∠А=∠С.
Что и требовалось доказать.
Пример 2: По данным рисунка докажите, что BО = ОD, АВ = CD, ∠B = ∠D.
Дано: AО = ОC, ∠A = ∠C.
Доказать: BО = ОD, АВ = CD, ∠B = ∠D.

Рис. 4. Чертеж к примеру 2
Доказательство:

Из равенства треугольников следует равенство их соответствующих элементов, а именно, что BО = ОD, АВ = CD, ∠B=∠D.
Что и требовалось доказать.
Пример 3: По данным рисунка найдите СD, АD, ∠С.
Дано ∠1 = ∠2, ∠3 = ∠4, ∠А = 60°, АВ = 6 см, ВС = 4 см.
Найти: СD, АD, ∠С.

Рис. 5. Чертеж к примеру 3
Доказательство:

Из равенства треугольников следует равенство их соответствующих элементов, а именно, что DC = AB = 6, AD = DC = 4, ∠C = ∠A = 60°.
Ответ: СD = 6 см, АD = 4 см, ∠С = 60°.
Домашнее задание
Выполнить в тетради, проверка будет по выходу в школу!
2. Докажите, что OB = OD. Известно, что ∠A = ∠C, AO = OC.

3. Докажите, что OВ = OА, если известно, что ∠D = ∠C, OC = OD.

4. На рисунке ∠DBC = ∠DAC, BO = AO. Докажите, что ∠C = ∠D.
