Каждому из вас известно, что в окружающем нас мире встречаются предметы, которые имеют одинаковую форму и одинаковые размеры. Например:
В геометрии две фигуры, имеющие одинаковую форму и одинаковые размеры, называют равными.
Давайте возьмём две фигуры F1 и F2, вырезанные из бумаги. Чтобы установить, равны они или нет, наложим одну фигуру на другую:

Предположим, что наши фигуры совместились, тогда можем сказать, что они равны.
А вот некоторые фигуры P1 и P2. Попробуем наложить их друг на друга:

Видим, что эти две фигуры совместить невозможно, а, следовательно, они не равны.
Вывод: две геометрические фигуры называются равными, если их можно совместить наложением.
Поговорим, как сравнить два отрезка. Возьмём два произвольных отрезка. Чтобы установить, равны они или нет, наложим один отрезок на другой так, чтобы конец одного отрезка совместился с концом другого. Если при этом совместились и два других конца отрезков, то можно сказать, что данные отрезки равны:

Теперь возьмём отрезок АВ и отрезок АС, и наложим их друг на друга таким же образом:

Видим, что отрезки не совместились полностью, а значит, они не равны.
Из рисунка также видно, что отрезок АВ составляет часть отрезка АС, поэтому АВ<АС.
Рассмотрим отрезок АВ. Отметим на нём точку С, которая делит его на две равные части:

Таким образом, можно сказать, что точка С — середина отрезка АВ, т.е. АС=СВ.
Определение:
Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка.
Рассмотрим два неразвёрнутых угла:

Чтобы установить, равны они или нет, наложим один угол на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместятся, то и углы полностью совместятся, а, значит, они равны:
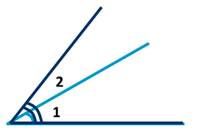
В нашем случае эти стороны не совместились, следовательно, наши углы не равны, и меньшим является угол, который составляет часть другого, а это угол 1. Запишем это так: угол 1<угла 2 (два).
Если мы возьмём неразвёрнутый угол АОС и развёрнутый угол ВОС, наложим их друг на друга указанным выше способом:
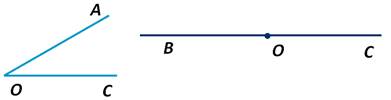
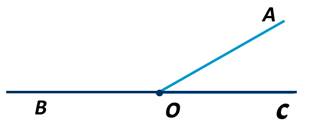
Видим, что неразвёрнутый угол составляет часть развёрнутого, а, следовательно, развёрнутый угол больше неразвёрнутого, т.е. угол ВОС больше угла АОС.
Следует отметить, что любые два развёрнутых угла, очевидно, равны:

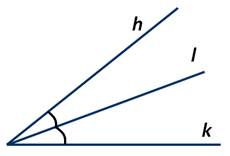
Возьмём некоторый угол hk. Проведём луч l из вершины этого угла так, чтобы он разделил его на два равных угла:
Определение:
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла. В нашем случае луч l — биссектриса угла hk.
Домашнее задание
Страница: 10 — 12 читать
Упражнения: 18 — 23