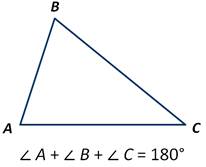
Теорема о сумме углов треугольника:

Сумма углов треугольника равна 180 градусов.

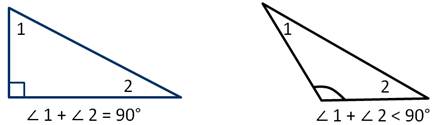
Из теоремы следует, что если в треугольнике один из углов является прямым или тупым, то сумма двух других углов данного треугольника не больше 90 градусов, а следовательно, каждый из них острый.

По величине углов выделяют следующие виды треугольников.

Определение:

Остроугольный треугольник — это треугольник, у которого все три угла острые.

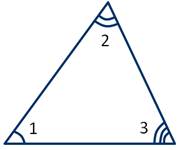
Определение:

Тупоугольный треугольник — это треугольник, у которого один из углов тупой.

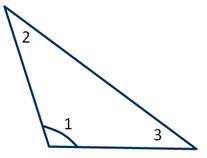
Определение:

Прямоугольный треугольник — это треугольник, у которого один из его углов является прямым.

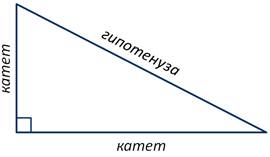
Нужно знать, что стороны прямоугольного треугольника имеют специальные названия.

Итак, две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

Если взять прямоугольный лист бумаги и разрезать его, получим:

Получим две модели прямоугольного треугольника.

Пример.

Доказать, что угол с вершиной на окружности, опирающийся на диаметр, — прямой.

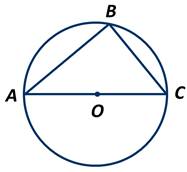
Для начала соединим точку В с точкой О, которая является центром нашей окружности. Так как отрезки ОА, ОВ и ОС равны как радиусы окружности, то треугольники АОВ и ВОС являются равнобедренными. А значит, у них углы при основаниях равны. Обозначим градусные меры этих углов m и n. Тогда ∠АОВ=2n, так как он является внешним углом треугольника ВОС, смежным с ∠ВОС. А нам известно, что внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

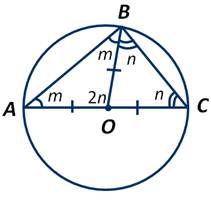
А так как сумма углов треугольника равна 180 градусов, то:

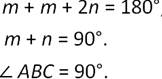
Что и требовалось доказать.

Пример.

Доказать, что если в равнобедренном треугольнике АВС один из углов равен 60 градусов, то он равносторонний.

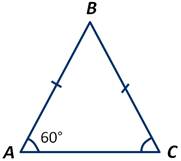
Если ∠А при основании равнобедренного треугольника АВС равен 60 градусов, то и второй ∠С при основании равен 60 градусам. Получаем:

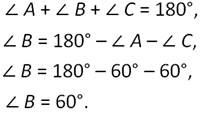
Следовательно, треугольник АВС равносторонний.

Пусть ∠В при вершине равнобедренного треугольника АВС равен 60 градусам. Тогда получим:

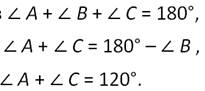
А так как углы А и С- углы при основании равнобедренного треугольника, то они равны между собой и равны 60 градусам. А следовательно, и в этом случае треугольник АВС является равносторонним. Что и требовалось доказать.

Пример.

Доказать, что в прямоугольном треугольнике АВС медиана, проведённая к гипотенузе АВ, равна половине гипотенузы.

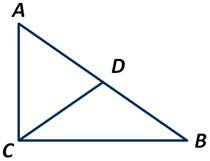
Отложив ∠2=∠1, получаем:

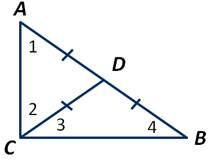
Треугольник ADC является равнобедренным. А следовательно, отрезок DA=DC.

Так как по условию угол АВС — прямой, то:

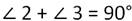
Известно, что сумма острых углов прямоугольного треугольника равна 90 градусов, то есть:

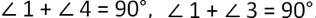
Тогда из равенств получаем:

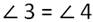
Из этого следует, что ВСD равнобедренный треугольник, у которого стороны DB и DC равны.

Следовательно, СD — медиана и СD равняется половине гипотенузы АВ. Что и требовалось доказать.

Свойства внешнего угла треугольника

ОПРЕДЕЛЕНИЕ

Угол, смежный с внутренним углом треугольника, называется внешним углом.

При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина.

Свойства внешнего угла

Внешний угол треугольника равен сумме внутренних углов не смежных с ним:
$\angle \text{1}=\angle A+\angle C$
Сумма внешнего и внутреннего углов при одной вершине равна ${180^{\circ}}$ :
$\angle \text{1}+\angle B={{180}^{\circ}}$
Сумма внешних углов треугольник взятых по одному при каждой вершине равна ${{360}^{\circ}}$ .
Внешние углы при одной вершине треугольника равны между собой (как вертикальные):
$\angle \text{1}=\angle 2$

Примеры решения задач

ПРИМЕР 1

Задание

В треугольнике $ABC$ углы $B$ и $C$ равны ${{65}^{\circ}}$ и ${{50}^{\circ}}$ соответственно. Найти внешние углы при каждой вершине треугольника.

Решение

Сумма углов треугольника $ABC$ равна ${{180}^{\circ}}$ , а значит

$\angle A={{180}^{\circ}}-\angle B-\angle C={{65}^{\circ}}$

Внешний угол при вершине $A$ равен сумме внутренних углов при вершинах $B$ и $C$ , т.е. ${{115}^{\circ}}$ . Аналогично получаем, что внешний угол при вершине $B$ равен ${{115}^{\circ}}$ , а внешний угол при вершине C равен ${{130}^{\circ}}$ .

Ответ

${{115}^{\circ}}, \quad {{115}^{\circ}}, \quad {{130}^{\circ}}$

ПРИМЕР 2

Задание

В треугольнике $ABC$ внешние углы при вершинах $B$ и $C$ равны ${{97}^{\circ}}$ и ${{125}^{\circ}}$ . Найти внутренний угол при вершине $A$ .

Решение

Обозначим внешний угол при вершине $B$ как $\angle 1$ , а внешний угол при вершине $C$ как $\angle 2$ (см. рисунок). Так как внешние и внутренние углы при одной вершине смежные (т.е. их сумма равна ${{180}^{\circ}}$ ), то

$\angle B={{180}^{\circ}}-\angle 1={{180}^{\circ}}-{{97}^{\circ}}={{83}^{\circ}}, \quad \angle C={{180}^{\circ}}-\angle 2={{180}^{\circ}}-{{125}^{\circ}}={{55}^{\circ}}$

Сумма углов треугольника $ABC$ равна ${{180}^{\circ}}$ , значит

$\angle A={{180}^{\circ}}-\angle B-\angle C={{180}^{\circ}}-{{83}^{\circ}}-{{55}^{\circ}}={{42}^{\circ}}$

Ответ

$\angle A={{42}^{\circ}}, \quad \angle B={{83}^{\circ}}, \quad \angle C={{55}^{\circ}}$

Теорема о внешнем угле треугольника

Прежде чем перейти к ранее не доказанным утверждениям, рассмотрим еще один полезный инструмент для доказательства различных фактов, связанных с треугольниками.

Если в треугольнике продолжить одну из сторон, то мы получим угол, смежный с одним из углов треугольника. Такой угол будем называть внешним углом треугольника (см. рис. 17), а углы внутри треугольника – внутренними.

Рис. 17. Внешний угол треугольника

Теорема 4 (о внешнем угле треугольника).

Внешний угол треугольника больше любого внутреннего, не смежного с ним.

На самом деле, мы уже знаем более сильное утверждение о внешнем угле. Сумма углов треугольника равна , поэтому внешний угол равен сумме двух внутренних, не смежных с ним:

Из этого очевидно следует, что он больше каждого из этих двух внутренних в отдельности.

Но мы не можем использовать для доказательства этой теоремы тот факт, что сумма углов треугольника равна , т. к. мы его пока формально не доказали. Более того, для того чтобы доказать теорему о сумме углов треугольника, мы будем использовать теорему о внешнем угле. Поэтому доказывать эту теорему мы будем только с использованием уже доказанных нами фактов. Как именно – можно почитать ниже.

Доказательство

Теорема (о внешнем угле треугольника)

Внешний угол треугольника больше любого внутреннего, не смежного с ним.

Доказательство

Самый разумный способом показать, что один угол больше другого, – это сравнить меньший угол с частью большего. Давайте попробуем. Продолжим сторону треугольника (см. рис. 18).