Определение:
Две прямые называют перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
Например, прямые АВ и СD образуют при пересечении четыре прямых угла, а значит, они являются взаимно перпендикулярными:
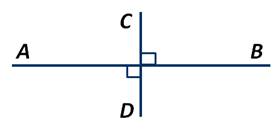
Перпендикулярность прямых АВ и CD обозначается следующим образом:
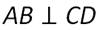
Отметим, что две прямые перпендикулярные к третьей не пересекаются.
Докажем это. Возьмём прямые АВ и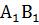 
перпендикулярные прямой СD:
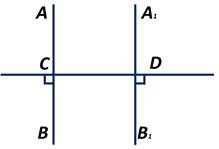
Перегнём рисунок по прямой СD так, чтобы верхняя часть рисунка наложилась на нижнюю. Так как прямые углы равны, то луч СА наложится на луч СВ, а луч D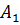
наложится на луч D
.
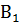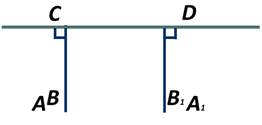
Если предположить, что АВ и 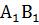пересекаются в некоторой точке О, то эта точка наложится на точку 
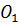, которая также лежит на этих прямых. Тогда мы получим, что через две точки О и 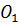проходят две прямые АВ и 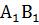, а это невозможно.
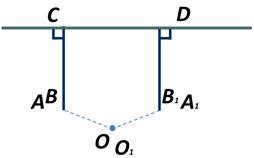
Следовательно, наше предположение неверно, а значит, прямые АВ и 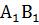не пересекаются.
Для проведения перпендикулярных прямых используют чертёжный треугольник с линейкой.
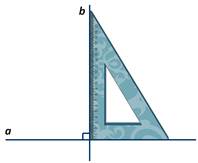
А вот, чтобы построить прямой угол на местности, можно воспользоваться простейшим прибором, который называют экер. Данный прибор представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков есть гвоздики, которые расположены так, что прямые проходящие через них взаимно перпендикулярны.
Чтобы построить прямой угол с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился над точкой О, а направление одного бруска совпало с направлением луча ОА. Затем провешивают линию по направлению другого бруска (прямая ОВ). В результате получается прямой угол АОВ.
В геодезии (в переводе с греческого «геодезия» означает «землеразделение»), науке, об измерениях на земной поверхности и в околоземном пространстве, для построения прямых углов используют наиболее совершенные приборы. Одним из таких является теодолит.
Домашнее задание
Страница: 22 – 24 п. 12-13 читать
Упражнения: 57, 65 – 70
