На предыдущем уроке мы говорили о четырёхугольнике. Напомним, что четырёхугольником называется геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. Причём никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
На этом уроке мы познакомимся с новой геометрической фигурой, которую называют параллелограммом.
Сформулируем определение: параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

Любой параллелограмм является выпуклым четырёхугольником.
Давайте посмотрим на следующие четырёхугольники.
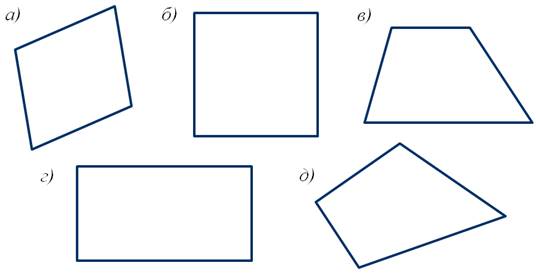
Первый является параллелограммом, так как у него противоположные стороны попарно параллельны. Следующий четырёхугольник также является параллелограммом, ведь у него противоположные стороны попарно параллельны. А вот четырёхугольник в пункте в не является параллелограммом, так как у него две стороны параллельны, а две другие – нет. У четырёхугольника в пункте г противоположные стороны попарно параллельны, а значит, он – параллелограмм. И последний четырёхугольник не является параллелограммом, так как у него стороны не параллельны.
Поговорим о свойствах параллелограмма.
Свойство 1. Сумма углов при соседних вершинах параллелограмма равна 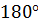 .
.
Доказательство.
Рассмотрим параллелограмм ABCD.

По определению параллелограмма стороны AB и CD параллельны, то есть лежат на параллельных прямых. Прямая AD, которая проходит через две соседние вершины, является секущей. А тогда углы BAD и ADC – внутренние односторонние.
Нам известно, что если две параллельные прямые пересечены секущей, то сумма односторонних углов равна ста восьмидесяти градусам. Следовательно, 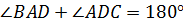 .
.
А так как эти углы являются углами при соседних вершинах параллелограмма, то свойство доказано.
Свойство 2. Диагональ разбивает параллелограмм на два равных треугольника.
Доказательство.
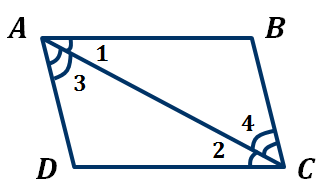
Рассмотрим 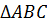 и
и 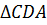 .
.
Сторона 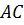 – общая,
– общая,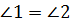 как накр. лежащие при
как накр. лежащие при 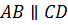 и секущей
и секущей 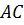 ,
,
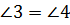 как накр. лежащие при
как накр. лежащие при 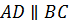 и секущей
и секущей 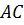 .
.
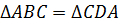 по второму признаку.
по второму признаку.
Что и требовалось доказать.
Свойство 3. У параллелограмма противоположные стороны равны.
Доказательство.
Рассмотрим параллелограмм ABCD.
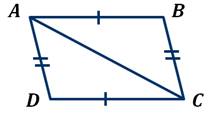
Диагональ AC разделяет его на два треугольника: ABC и CDA. Доказывая предыдущее свойство, мы выяснили, что эти треугольники равны, то есть у них соответствующие стороны равны. И сторона AB = DC, а сторона AD = BC.
Свойство доказано.
Свойство 4. У параллелограмма противоположные углы равны.
Доказательство. Рассмотрим параллелограмм ABCD. Проведём диагональ AC.
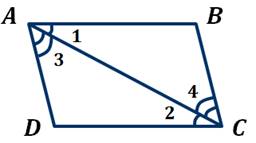
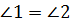
как накр. лежащие при 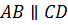 и секущей
и секущей 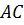 ,
,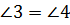 как накр. лежащие при
как накр. лежащие при 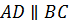 и секущей
и секущей 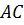 ,
,
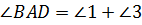 ,
,
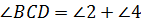 ,
,
следовательно, 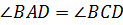 .
.
Что и требовалось доказать.
Также равенство противоположных углов параллелограмма следует из равенства треугольников ABC и CDA, которое мы доказали в предыдущем свойстве.
Свойство 5. Диагонали параллелограмма точкой пересечения делятся пополам.
Доказательство. Рассмотрим параллелограмм ABCD. Пусть точка О – точка пересечения диагоналей AC и BD.
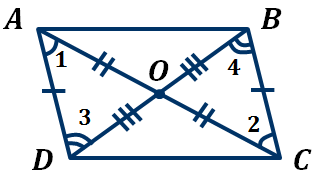
Рассмотрим 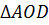 и
и 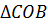 .
.
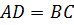 как противоположные стороны,
как противоположные стороны,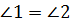 как накр. лежащие при
как накр. лежащие при 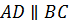
и секущей 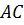 ,
,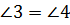 как накр. лежащие при
как накр. лежащие при 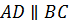 и секущей
и секущей 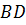 .
.
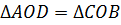 по второму признаку.
по второму признаку.
Следовательно, 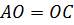 ,
,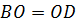 .
.
Что и требовалось доказать.
Теперь для закрепления материала решим несколько задач.
Задача. Докажите, что биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Доказательство. Пусть ABCD – некоторый параллелограмм. Проведём, например, из вершины А биссектрису АМ.
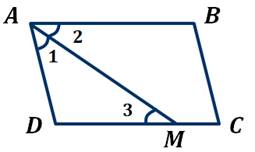
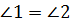 ,так как
,так как 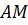 – биссектриса.
– биссектриса.
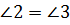 как накр. лежащие при
как накр. лежащие при 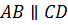 и секущей
и секущей 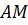 .
.
Следовательно, 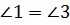 .
.
Тогда 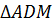 – равнобедренный.
– равнобедренный.
Задача. У параллелограмма 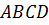 диагональ
диагональ 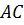 равна 16 см, диагональ
равна 16 см, диагональ 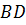 – 10 см, а сторона
– 10 см, а сторона 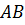 – 8 см. Найдите периметр треугольника
– 8 см. Найдите периметр треугольника 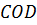 .
.
Решение.
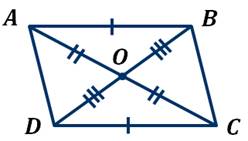
Рассмотрим 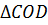 .
.
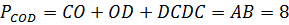 (см),
(см),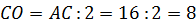 (см),
(см),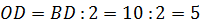 (см).
(см).
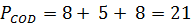 (см).
(см).
Ответ: 21 см.