Для начала решим задачу, которая поможет повторить всё, что мы знаем о векторах.
Итак, ABCD — параллелограмм.
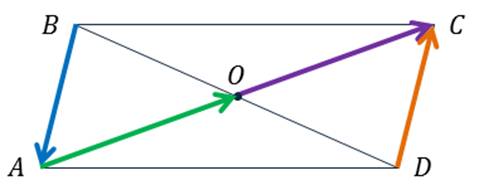
Нам предстоит назвать все векторы, которые изображены на рисунке, и указать среди них: равные по длине, коллинеарные, сонаправленные, противоположно направленные, равные и векторы сонаправленные вектору ОО.
Чтобы назвать векторы, изображённые на рисунке, повторим определение понятия вектора.
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
На рисунках вектор изображают в виде отрезка со стрелкой, показывающей направление вектора.
Называют векторы двумя заглавными буквами со стрелкой над ними. При этом первая буква обозначает начало вектора, а вторая — конец.
По порядку назовём изображённые векторы: 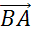 ,
, 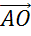 ,
, 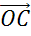 ,
, 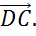 Далее среди них найдём равные по длине. Стоит вспомнить, что длиной ненулевого вектора
Далее среди них найдём равные по длине. Стоит вспомнить, что длиной ненулевого вектора 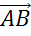 называется длина отрезка AB.
называется длина отрезка AB.
Пользуясь тем, что перед нами параллелограмм, можем сказать, что его противоположные стороны равны. А также диагонали точкой пересечения делятся пополам.
А значит, равны длины векторов 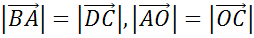 .
.
Теперь укажем коллинеарные векторы. Ненулевые векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.
Мы знаем, что противоположные стороны параллелограмма не только равны, а ещё и параллельны. Поэтому коллинеарными будут векторы 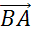 и
и 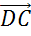 .
.
Ну, а векторы 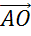 и
и 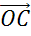 коллинеарны, так как лежат на одной прямой.
коллинеарны, так как лежат на одной прямой.
Далее нам предстоит отыскать сонаправленные и противоположно направленные векторы.
Сонаправленными называют ненулевые коллинеарные векторы с одинаковыми направлениями.
Противоположно направленными называют ненулевые коллинеарные векторы с противоположными направлениями.
В обоих случаях векторы должны быть коллинеарны.
Мы же с вами указали только две пары коллинеарных векторов. Из них сонаправленными будут векторы 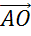 и
и 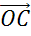 , а противоположно направленными — векторы
, а противоположно направленными — векторы 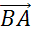 и
и 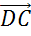 .
.
Далее вспомним определение равных векторов. Векторы называют равными, если они сонаправлены и их длины равны.
Ранее нами указана только одна пара сонаправленных векторов, между тем их длины равны. Значит, вектор 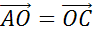 .
.
В последнем пункте укажем векторы сонаправленные вектору ОО.
Такой вектор на рисунке не изображён, но с прошлых уроков вам известно понятие нулевого вектора.
Любая точка плоскости является нулевым вектором. Длина любого нулевого вектора равна нулю.
Так как начало и конец у такого вектора совпадают, то у него нет определённого направления и его можно задать любым направлением. Поэтому нулевой вектор считается сонаправленным любому вектору.
Тогда мы можем сказать, что каждый из векторов 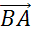 ,
, 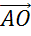 ,
, 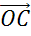 ,
, 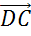 сонаправлен вектору ОО.
сонаправлен вектору ОО.
В ходе выполнения данного задания мы повторили всё, что знаем о векторах. Теперь приступим к изучению новой темы.
Если точка А является началом вектора А, то говорят что вектор А отложен от точки А.
Имеет место следующее утверждение. От любой точки 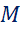 можно отложить вектор, равный данному вектору
можно отложить вектор, равный данному вектору 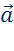 , и притом только один.
, и притом только один.
Доказательство.
Рассмотрим два случая.
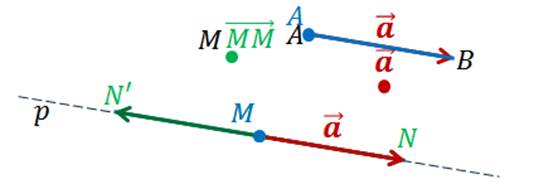
1. 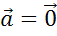 , то искомым, равным ему, вектором будет вектор
, то искомым, равным ему, вектором будет вектор 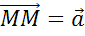 .
.
2. 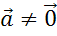 , а точки А и B — его начало и конец, то через точку М проведём прямую p параллельную AB:
, а точки А и B — его начало и конец, то через точку М проведём прямую p параллельную AB: 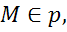
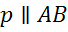 .
.
Теперь отложим отрезки MN и MN’, равные отрезку AB: 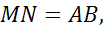
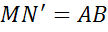 .
.
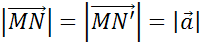
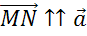
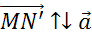
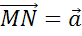
Из построения видно, что такой вектор только один.
Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой.
Поэтому вектор 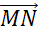 можно обозначить как вектор
можно обозначить как вектор 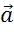 .
.
Про такие векторы можно сказать, что это один и тот же вектор, но отложенный от разных точек.
Отложить векторы, равные ненулевому вектору 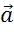 , от каждой из вершин
, от каждой из вершин 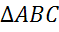 .
.
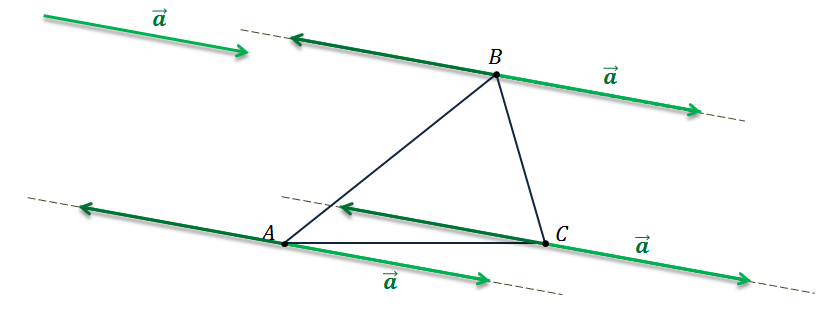
Для этого через каждую вершину проведём прямые параллельные вектору 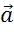 .
.
По каждую сторону от точек А, B и C на этих прямых отложим отрезки равные длине вектора 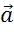 . Таким образом получим по два вектора у каждой из вершин.
. Таким образом получим по два вектора у каждой из вершин.
Но один из них будет сонаправлен вектору 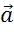 , а другой — противоположно направлен.
, а другой — противоположно направлен.
Нам подойдут вектора сонаправленные вектору 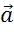 .
.
Так мы отложили от каждой вершины треугольника ABC векторы, равные вектору 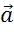 .
.
Задача. От точки 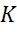 необходимо отложить вектор:
необходимо отложить вектор:
а) равный вектору 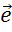 ;
;
б) сонаправленный вектору 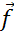 ;
;
в) противоположно направленный вектору 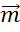 .
.
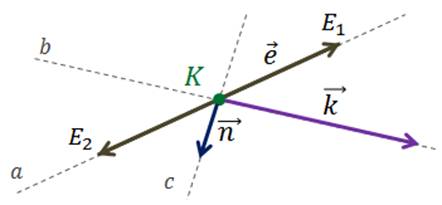

Отложим от К вектор равный вектору 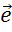 . Для этого через точку К проведём прямую a, параллельную вектору
. Для этого через точку К проведём прямую a, параллельную вектору 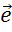 .
.
От точки К на данной прямой отложим отрезки, длины которых равны длине вектора 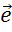 . Получаем два вектора. Выберем тот, который сонаправлен с вектором
. Получаем два вектора. Выберем тот, который сонаправлен с вектором 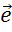 .
.
Так мы отложили от точки К вектор, равный вектору 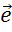 . Можем его так же обозначить как вектор
. Можем его так же обозначить как вектор 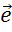 .
.
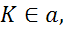
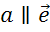
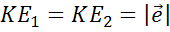
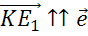
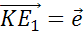
Далее отложим от точки К вектор сонаправленный с вектором 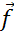 .
.
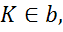
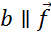
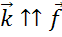 .
.
Последним необходимо от точки К отложить вектор противоположно направленный вектору 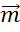 .
.
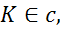
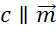
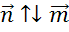
Перейдём к решению последней задачи.
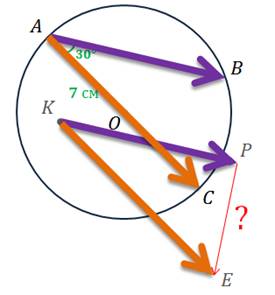
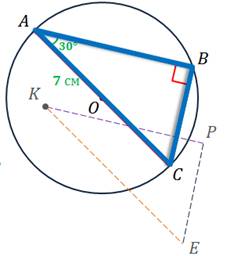
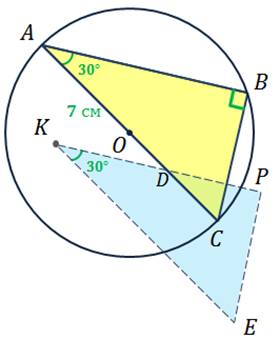
Задача. Диаметр 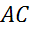 и хорда
и хорда 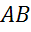 окружности образуют угол в
окружности образуют угол в 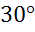 , а радиус окружности равен
, а радиус окружности равен 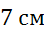 . Внутри данной окружности выбрана точка
. Внутри данной окружности выбрана точка 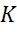 и от неё отложены векторы
и от неё отложены векторы 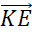 и
и 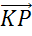 равные векторам
равные векторам 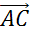 и
и 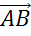 соответственно. Найти
соответственно. Найти 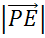 .
.
Решение.
1. 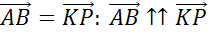 (
(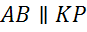 )
)
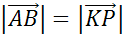 (
(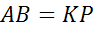 )
)
2. 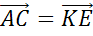 :
: 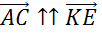 (
(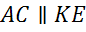 )
)
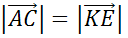 (
(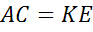 )
)
3. 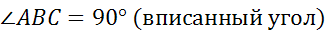
3. 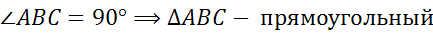
4. 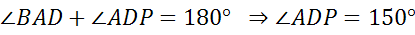
односторонние при 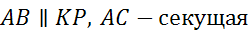
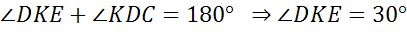
односторонние при 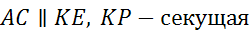
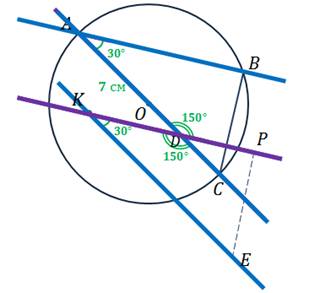
5. 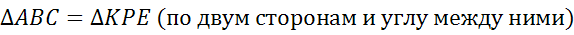 .
.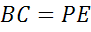
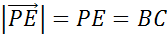
6. 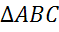 :
: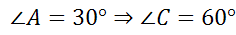
7. 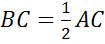
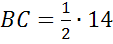
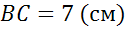
8. 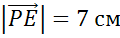
Подведём итоги нашего урока.
Сегодня вы узнали, что от любой точки М можно отложить вектор, равный данному вектору 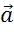 , и притом только один. Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Про такие векторы можно сказать, что это один и тот же вектор, но отложенный от разных точек.
, и притом только один. Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Про такие векторы можно сказать, что это один и тот же вектор, но отложенный от разных точек.