Из физики вам известно, что некоторые величины характеризуются не только числовым значением, а ещё и направлением. Их называют векторными величинами.
Рассмотрим одну из таких величин, а именно скорость.
Пусть из пунктов А и Б одновременно навстречу друг другу движутся мотоциклист и гружёный грузовик.

Их скорости обозначены отрезками со стрелками, которые указывают направление движения.
Исходя из того, что отрезок, обозначающий скорость мотоциклиста, длиннее, можно сделать вывод, что скорость мотоциклиста больше скорости грузовика.
На таком наглядном примере легко увидеть свойства физических векторных величин: числовое значение и направление.
Теперь перейдём к геометрическому понятию вектора.
Рассмотрим произвольный отрезок АБ. Точки А и Б называют его концами или граничными точками.

Итак, на данном отрезке можно указать два направления: от точки B к точке А и наоборот.
Чтобы выбрать только одно направление, назовём одну граничную точку началом отрезка, а другую — концом отрезка. Будем считать, что отрезок направлен от начала к концу.

Запишем определение. Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
На рисунках вектор изображают в виде отрезка со стрелкой, показывающей направление вектора. Обозначают вектор двумя заглавными буквами со стрелкой над ними, например 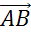 .
.
При этом первая буква обозначает начало вектора, а вторая — конец.
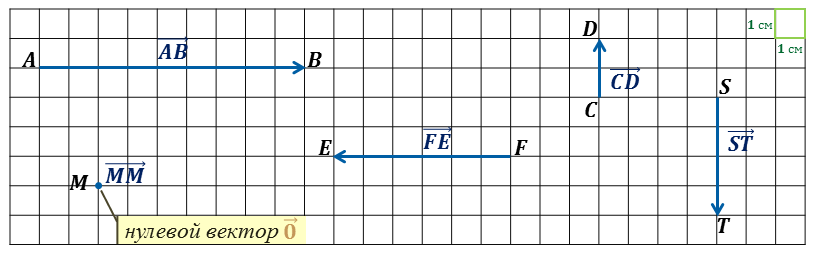
Условимся любую точку плоскости также считать вектором. Тогда вектор обозначенный точкой М будет иметь название 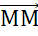 . Такие вектора будем называть нулевыми и обозначать их можно таким символом.
. Такие вектора будем называть нулевыми и обозначать их можно таким символом.
Также вектора иногда называют одной строчной латинской буквой со стрелкой над ней. Например,  ,
, 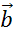 ,
, 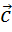 ,
, 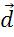 ,
, 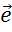 .
.
Длиной ненулевого вектора 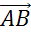 называется длина отрезка
называется длина отрезка 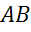 . Длину вектора
. Длину вектора 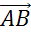 обозначают так
обозначают так 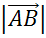 . Можно говорить «модуль вектора АБ». Находя длину вектора, мы не учитываем его направление.
. Можно говорить «модуль вектора АБ». Находя длину вектора, мы не учитываем его направление.
Учитывая, что каждая клетка имеет сторону длиной в 1 сантиметр, получаем, что
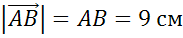 ,
, 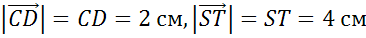 ,
, 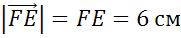 ,
, 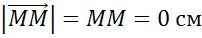 .
.
Длина любого нулевого вектора равна нулю 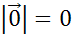 .
.
Вот вы и познакомились с понятием вектора. Теперь можно приступить к решению задач.
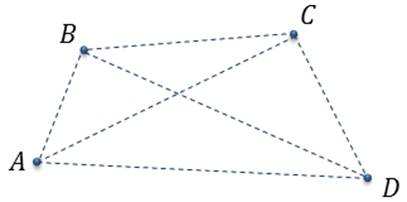
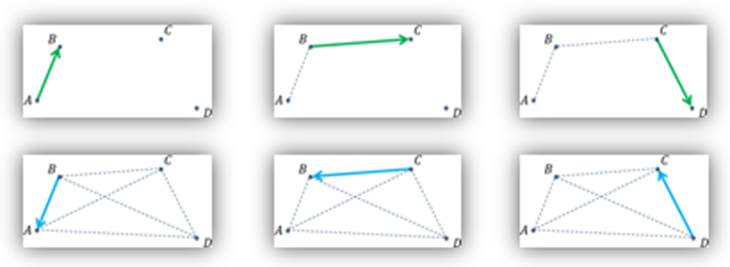
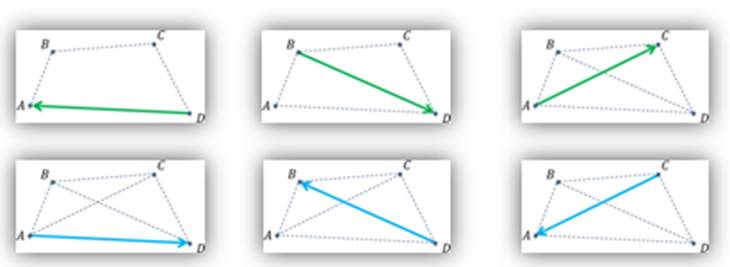
Задача. Отметить точки 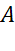 ,
, 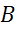 ,
, 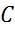 и
и 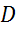 так, чтобы никакие
так, чтобы никакие  из них не лежали на одной прямой. Начертить все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек. Выписать все полученные векторы и указать их начало и конец.
из них не лежали на одной прямой. Начертить все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек. Выписать все полученные векторы и указать их начало и конец.
Решение.

Задача. В треугольнике 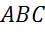 стороны
стороны 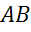 ,
,  и
и 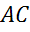 равны
равны 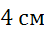 ,
, 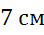 и
и 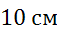 .
.
Точки 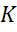 ,
, 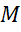 и
и 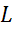 — середины сторон
— середины сторон 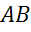 ,
, 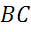 и
и 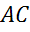 треугольника.
треугольника.
Найти длины векторов 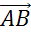 ,
, 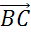 ,
, 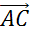 ,
, 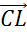 ,
, 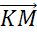 ,
, 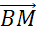 и
и 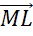 .
.
Решение.
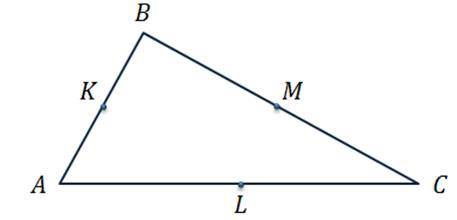
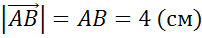
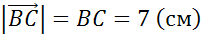
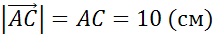
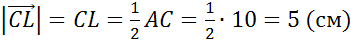
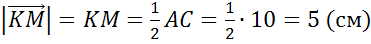
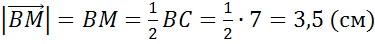
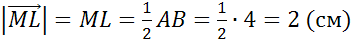
Решим последнюю задачу.
Задача. Стороны прямоугольника 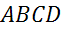 равны
равны 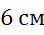 и
и 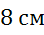 . Найти длину вектора
. Найти длину вектора 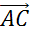 .
.
Решение.
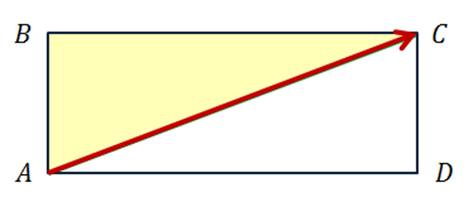
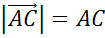
Рассмотрим  прямоугольный
прямоугольный
по теореме Пифагора 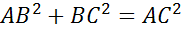
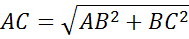
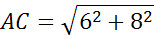
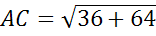
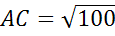
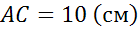
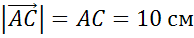
Ответ: 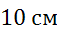 .
.
Подведём итоги урока.
Сегодня вы познакомились с понятием вектора. Это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. Ещё вектор называют направленным отрезком.
Обозначают вектор двумя заглавными буквами со стрелкой над ними, например 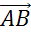 . При этом первая буква обозначает начало вектора, а вторая — конец.
. При этом первая буква обозначает начало вектора, а вторая — конец.
Также вектора иногда называют одной строчной латинской буквой со стрелкой над ней.
Любая точка плоскости так же является вектором. Такой вектор называют нулевым и обозначают так 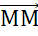 .
.
Длиной или модулем ненулевого вектора 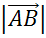 называется длина отрезка АB.
называется длина отрезка АB.
Длина любого нулевого вектора равна 0.