Информационные модели на графах. Использование графов при решении задач. ПР №14 «Создаём информационные модели – схемы, графы, деревья» (зад 4 и 6)

Вопросы занятия:

· граф;

· дерево;

· иерархия.

На прошлых уроках мы с вами узнали об информационных моделях, которые в сжатой форме помогают представлять информацию и решать задачи.

Давайте вспомним:

Сделать табличную информацию более наглядной и легко доступной помогают графики и диаграммы.

График – это линия, применяемая для наглядного изображения зависимости одной какой-либо величины от другой.

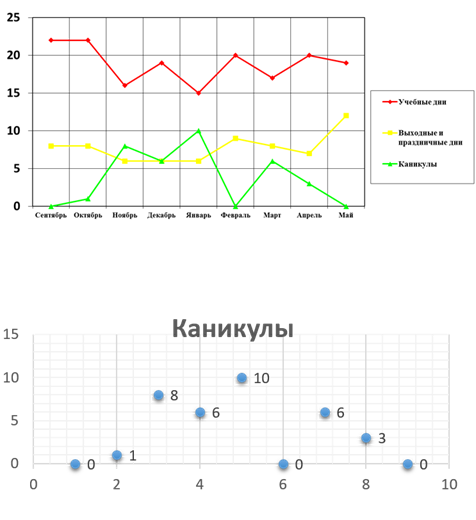
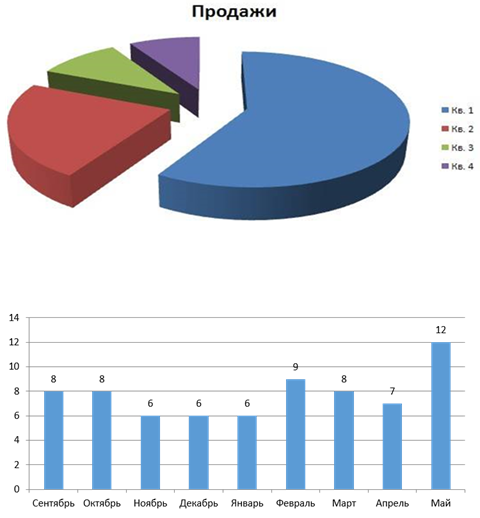
Диаграмма – это чертёж, показывающий соотношение нескольких величин. В зависимости от цели можно использовать разные типы диаграмм. Например, круговые или столбчатые.

Следующий вид графических средств представления информации – схемы.

Схема – это информационная модель, в которой с помощью особых приемов и географических обозначений выделяется один или несколько признаков рассматриваемого объекта.

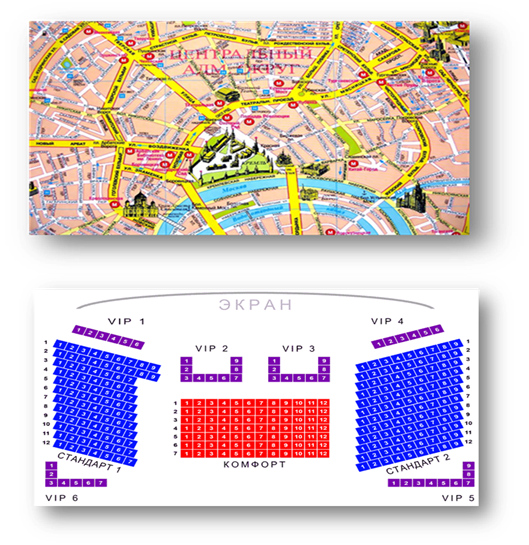
Есть ещё один вид графических средств – это графы.

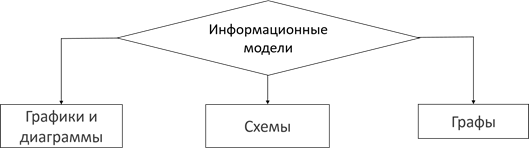
Сегодня на уроке мы узнаем:

Какие информационные модели называются графами, для чего применяются графы, и как с помощью графов решать задачи.

Граф — это группа объектов со связями между ними.

Объекты представляются как вершины графа, а связи — это линии соединяющие вершины.

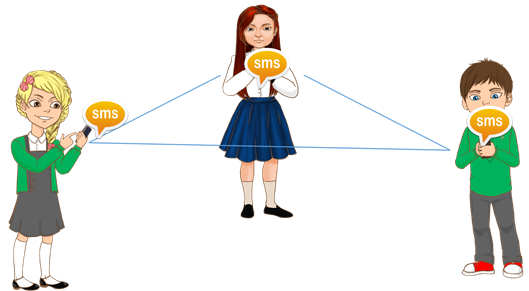
Например, все шестиклассники пользуются мобильными телефонами и многие общаются друг с другом через SMS.

В данном примере вершины графа – это отдельные ребята, а связи – это процесс «пишут друг другу SMS».

Вершины графа можно изображать по-разному. Это может быть овал либо круг, точка или прямоугольник.

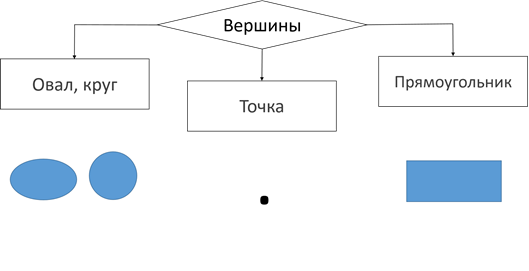
Разберёмся более подробно со связями, то есть с линиями, соединяющими вершины графа.

Дуга

Если линия, соединяющая вершины графа направленная, то есть со стрелкой, то она называется дугой.

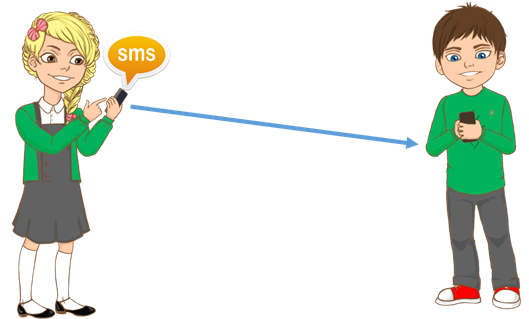
То есть дугой называется направленная линия, соединяющая вершины графа.

Ребро

Если линия ненаправленная, то есть, нет стрелки, то эта линия называется ребром.

Ребро – это ненаправленная линия, которая соединяет вершины графа.

Петля

Если линия выходит из некоторой вершины и входит в неё же, то эта линия называется петлёй.

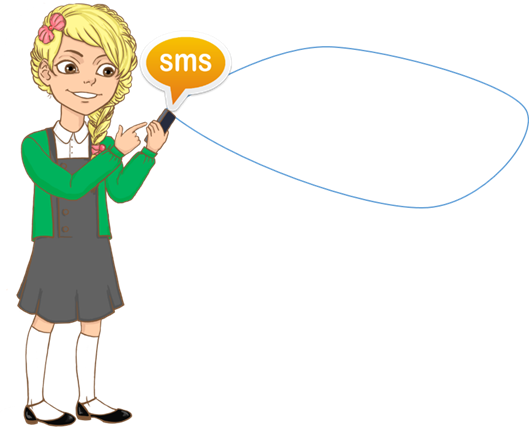
Петля – это линия, которая выходит из некоторой вершины и входит в нее же

Вернёмся к примеру, с шестиклассниками. Здесь система – это ученики шестого класса в какой-то школе. Мы, объекты этой системы (т.е. отдельных ребят) изобразили вершинами, и соединили вершины ненаправленными линиями (рёбрами). Ребра в данном случае являются двухсторонними отношениями, потому что ребята пишут SMS-ки друг другу.

Мы получили информационную модель рассматриваемой системы в форме графа.

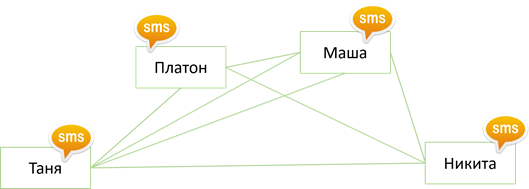
Рассмотрим виды графов.

Если вершины графа соединены рёбрами, то такой граф называется неориентированным.

Рассмотрим пример: Таня написала SMS Никите, Никита ответил Тане, Таня написала Маше, Маша ответила Тане, Никита написал Маше. Здесь ребята отвечали друг другу на смски.

Данное отношение называется цепью графа.

Цепь графа – это путь по вершинам и рёбрам графа, который включает любое ребро не меньше одного раза.

Если в цепи начальная и конечная вершины совпадают, то такая цепь называется циклом.

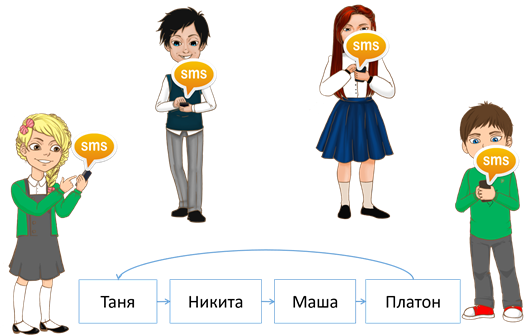
Например, Таня написала SMS Никите, Никита – Маше, Маша – Платону, а Платон написал Тане.

Здесь цикл – это цепь Таня – Никита – Маша – Платон – Таня.

Далее, рассмотрим следующий вид графа.

Если вершины графа соединены дугами (стрелками), то такой граф называется ориентированным.

В нашем примере цепь будет выглядеть следующим образом: Таня написала SMS Никите, Никита – Маше, Маша – Платону. То есть СМС-ки были без ответа.

Рассмотрим следующий пример:

Город Москва основан в 1147 году, город Санкт-Петербург основан в1703 году. Расстояние от Москвы до Санкт-Петербурга 713 км. Год основания города Тверь 1135 год, расстояние от Москвы до Твери 175 км. Ярославль основан в 1010 год, расстояние от Москвы до Ярославля 272 км. Город Смоленск основан в 863 году, а расстояние от Москвы до Смоленска 400 км.

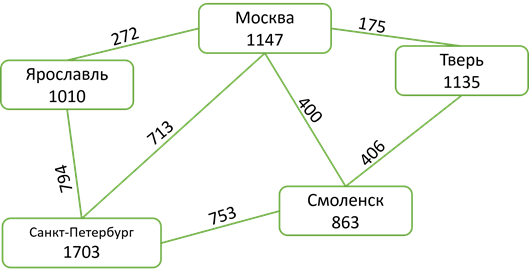
Мы получили взвешенный граф.

Взвешенным называется граф, который характеризуется дополнительной информацией – весом вершины или весом ребра (дуги).

Рассмотрим следующий вид графа с циклами, то есть граф, в цепи которого начальная и конечная вершины совпадают.

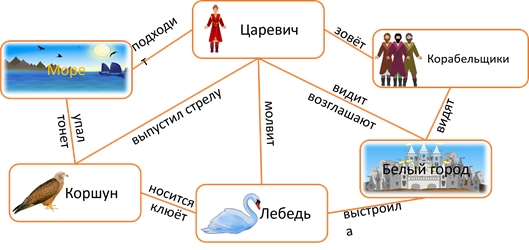
Помните сказку о царе Солтане? Давайте построим граф по отрывкам из сказки.

К морю лишь подходит он,

Вот и слышит будто стон…

Бьётся лебедь средь зыбей,

Коршун носится над ней;

Но как раз стрела запела,

В шею коршуна задела —

Коршун в море кровь пролил,

Лук царевич опустил;

Смотрит: коршун в море тонет

И не птичьим криком стонет,

Лебедь около плывёт,

Злого коршуна клюёт,

И царевичу потом

Молвит русским языком…

Вот открыл царевич очи;

Отрясая грёзы ночи

И дивясь, перед собой

Видит город он большой,

Мать и сын идут ко граду.

Лишь ступили за ограду,

Пышный двор встречает их;

Все их громко величают

И царевича венчают

Княжий шапкой, и главой

Возглашают над собой…

И так далее.

Мы получили граф с циклами, который называется сетью. Если раньше мы рассматривали примеры, в которых связи были одинаковые (ребята писали смски), то в данном примере связи различны. Поэтому мы их подписывали.

Следующий вид графа, называется дерево.

Дерево – это граф с иерархической системой, где Иерархия – это структура распределения частей целого от высшего к низшему. А Иерархическая система – это система, части которой находятся в определённых отношениях. К отношениям иерархической системы относятся «является разновидностью», «входит в состав» и другие «отношения подчинённости».

Рассмотрим иерархическую систему фирмы, которая, например, занимается реализацией техники. Здесь будет такая система подчинённости: генеральный директор — самый главный человек и владелец фирмы, ему подчиняются директора магазинов, которые руководят работой администраторов, ну а тем, в свою очередь, подчиняются продавцы.

Рассмотрим систему, связанную системой подчинённости «входят в состав». Она имеет иерархическую структуру. Например, изобразим следующий граф иерархической системы:

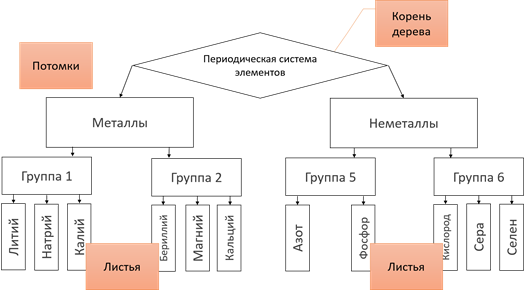
Периодическая система элементов в неё состав входят металлы и неметаллы. В свою очередь металлы делятся на 2 группы – группа 1 и группа 2, неметаллы делятся также на 2 группы – группа 5 и группа 6 и так далее. В отличие от остальных графов дерево не содержит циклов и петель, так как между любыми двумя его вершинами существует только один путь.

Так же у графа «Дерево» выделяется главная вершина, которая называется корень дерева. У любой вершины дерева могут быть потомки. А вершины, у которых нет потомков, называются листьями.

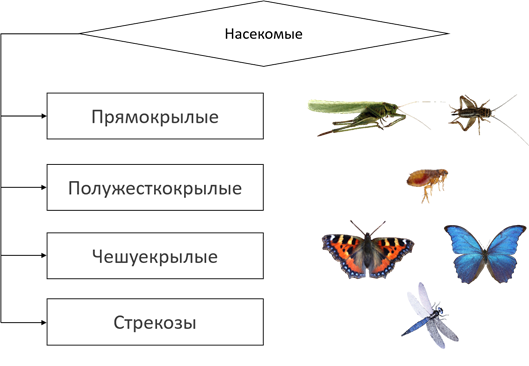
Следующий вид древовидного графа с отношением «является разновидностью» применяется для представления классификации объектов.

Например, разновидностями отряда «Насекомые» являются: Прямокрылые к ним относятся кузнечики, сверчки. Полужёсткокрылые – к ним относятся клопы, Чешуекрылые к ним относятся бабочки и Стрекозы.

Некоторые виды задач удобно решать с помощью графов.

Давайте решим одну из задач.

В коробке три шарика: жёлтый, зелёный и красный. Шестиклассница Таня со своими двумя друзьями Машей и Никитой вынимают их из коробки по одному. Сколько комбинаций выбора при этом возможно? Нужно выписать все варианты выбора.

Решение данной задачи удобно представить в виде дерева. Возьмём за корневую вершину произвольную току О., Таня может взять из коробки один из трёх шариков. Обозначим их буквами Ж, З и К. На схеме это соответствует трём ветвям, исходящим из точки О. Первый уровень в нашей задаче – это выбор Тани.

Теперь мы будем строить второй уровень графа. Второй уровень – это выбор Никиты.

Если Таня взяла жёлтый шарик, то Никита может взять зелёный или красный. Если же Таня взяла зелёный шарик, то Никита может взять жёлтый или красный. Аналогично, если Таня взяла красный шарик, то Никита может взять жёлтый или зелёный.

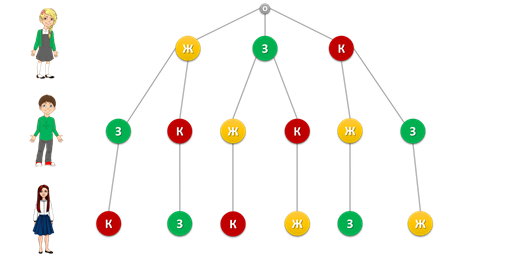
Осталось построить третий уровень, который отображает выбор Маши. Маша в каждом случае может взять оставшийся шарик. То есть если Таня взяла жёлтый шарик, а Никита зелёный, то Таня возьмёт красный шарик. Следующий вариант: если Таня взяла жёлтый шарик, а Никита Красный, Маша возьмёт зелёный шарик. И так далее мы достраиваем оставшиеся ветви.

Выпишем все пути от вершин первого уровня к вершине третьего. Каждый из выписанных путей определяет один из вариантов вытягивания шестиклассниками шариков из коробки. Так как других путей нет, то искомое число вариантов – 6.

Если при решении задачи не нужно указывать все возможные варианты, а нужно просто указать их число, то дерево можно и не строить. Тогда рассуждаем так: Таня может взять один из трёх шариков, Никита может взять один из двух оставшихся шариков, а Маша – один оставшийся. Получаем: 3, умножить на 2, умножить на 1 получаем ответ – 6 вариантов.

Итак, сегодня на уроке мы узнали:

Граф является наглядным средством представления информации состава и структуры системы.

Дерево – это граф с иерархической системой. Отличительная особенность дерева – это то, что между любыми двумя вершинами существует единственный путь.

Иерархия – это структура распределения частей целого от высшего к низшему.

Иерархическая система – это система, части которой находятся в отношениях подчинённости «является разновидностью», «входит в состав» и других.

Перейдём к практической части урока.

Сегодня на уроке мы научимся:

пользоваться инструментом Надпись

добавлять (вписывать) текст в автофигуру

строить схемы.

1-e задание. Солнечная система.

1. Открыть текстовый документ «Солнечная система.docx».

2. На картинке по информации из таблицы указать положение планет.

3. Сохранить документ под именем «Солнечная система надписи».

Приступим.

Открываем в своей рабочей папке документ Солнечная система.docx. Здесь мы видим схему солнечной системы, по информации из таблицы, нам нужно указать положение планет.

Для этого:

Смотрим внимательно на схему и таблицу.

Ближе всего к солнцу находится Меркурий. Обозначим на схеме Меркурий.

Выбираем вкладку Вставка, затем в группе Текст выберем инструмент Надпись, и нажимаем Нарисовать надпись, при этом указатель мыши примет форму «плюса».

Чтобы вставить надпись стандартного размера просто щёлкните в документе.

Если размер надписи нужно изменить поднесите мышку к любому из маркеров в прямоугольнике и растяните до нужного размера.

Перетащим надпись на нужное место.

Если надпись окружена рамкой, уберём рамку. Нажимаем Формат – Контуры фигуры – Нет контура.

Аналогично подпишем остальные планеты солнечной системы.

Сохраним результат работы в своей рабочей папке под именем Солнечная система надписи.

2-e задание. Поездка в автобусе.

1. Открыть текстовый документ «Поездка в автобусе.docx».

2. Дорисовать схему отношений при поездке в автобусе и подписать их названия с помощью глаголов.

3. Сохранить документ под именем «Поездка в автобусе граф».

Открываем файл Поездка в автобусе.docx в своей рабочей папке. Здесь мы видим незаконченную схему отношений при поездке в автобусе, дорисуем её и подпишем отношения с помощью глаголов. Для этого:

Смотрим на схему. Водитель ведёт автобус.

Выбираем вкладку Вставка, в группе Иллюстрации нажимает на Фигуры. Здесь нам нужна стрелка. Соединяем вершины графа Водитель – Автобус стрелкой и, также как в первом задании, добавляем надпись.

Аналогично достраиваем всю схему.

Сохраним результат работы в своей рабочей папке под именем Поездка в автобусе граф.

Третье задание называется Арифметические выражения.

1. Открыть текстовый документ «Арифметические выражения.docx».

2. По данному образцу построить дерево для арифметического выражения.

3. Сохранить документ под именем «Выражение дерево».

Открываем файл Арифметические выражения.docx в своей рабочей папке. Здесь мы видим образец дерева для арифметического выражения. С помощью вкладки Вставка – Автофигуры построим дерево для нашего арифметического выражения.

Листьями данного дерева являются числа, а остальные вершины – это арифметические операции. Листья связаны с вершинами рёбрами.

Сохраним свою работу в своей рабочей папке под именем Выражение дерево.

Таким образом, сегодня на уроке мы научились:

• пользоваться инструментом Надпись;

• добавлять (вписывать) текст в автофигуру;

• строить разнообразные схемы.

Задание 4

1. Рассмотрите граф, представляющий процесс вычисления арифметического выражения 5 х (3 + 7) х (8 — 2):

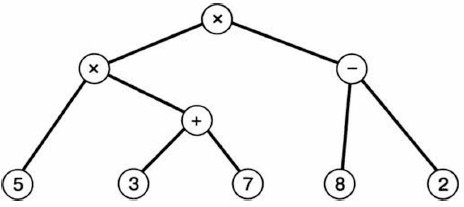
Рассмотрите граф

Это дерево, листьями которого являются числа, а прочими вершинами — операции. Дуги связывают вершину-операцию с вершинами-операндами.

2. Постройте аналогичное дерево для арифметического выражения 6 х 4 + 7 х (9 — 1).

3. Сохраните результат работы в личной папке под именем Выражение.

Наши конкурсы

Задание 5

1. Рассмотрите файловую структуру диска, на котором записаны работы участников школьных конкурсов по информационным технологиям (см. с. 96).

2. Средствами текстового процессора создайте соответствующую схему.

3. Сохраните результат работы в личной папке в файле с именем Конкурсы.

Царство животных

Задание 6

1. Составьте схему по следующему описанию:

Близкие виды объединяются в один род. Например: ворона, ворон, галка и грач объединены в род Ворон. Близкие роды объединяются в семейства: род Ворон, род Сорока, род Сойка, род Кедровка объединены в семейство Вороновые. В свою очередь, близкие семейства объединяются в отряды. Так, семейство Синицевые, семейство Вороновые, семейство Ласточковые принадлежат отряду Воробьинообразные. Близкие отряды составляют класс. Так, отряд Воробьинообразные, отряд Совооб- разные, отряд Гусеобразные принадлежат к классу Птицы. Близкие классы объединены в типы. Так, класс Птицы, класс Амфибии, класс Млекопитающие входят в тип Хордовые. В настоящее время выделяют до 25 различных типов животных. Все они объединены в царство Животные.

2. Сохраните результат работы в личной папке в файле с именем Животные.

Круги Эйлера

Задание 6

1. Постройте схему, на которой кругами обозначьте три множества: множество всех высоких людей; множество всех пап; множество родителей, умеющих плавать. Подпишите эти множества.

2. Закрасьте жёлтым цветом область, которая обозначает множество всех высоких пап, умеющих плавать, и сделайте соответствующую надпись.

3. Закрасьте синим цветом область, которая обозначает множество всех высоких пап, не умеющих плавать, и сделайте соответствующую надпись.

4. Закрасьте красным цветом область, которая обозначает множество всех невысоких мам, умеющих плавать, и сделайте соответствующую надпись.

5. Сохраните схему в личной папке под именем Круги_Эйлера.