Осевая симметрия в математике, природе, архитектуре
Как на занятиях аппликацией вырезать бабочку, елочку или кленовый лист, чтобы обе половинки изделия были одинаковыми? Нужно свернуть цветную бумагу пополам, нарисовать половинку необходимой фигуры, вырезать и развернуть. Получится изделие, у которого обе половинки абсолютно одинаковы, каждая является зеркальным отражением другой. При разгибании одна половинка совершает поворот на 1800. В данном случае поворот совершается относительно линии сгиба, которая является осью. Таким образом, мы получили симметричные фигуры относительно оси. Говорят, что в этом случае имеет место осевая симметрия. А о фигурах, которые можно перегнуть так, что их половинки совпадут, говорят, что они имеют ось симметрии или что они симметричны относительно оси (линии сгиба).
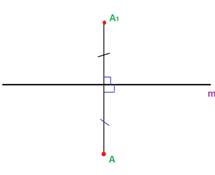
Выполним практическое задание. Даны прямая m и точка А, не принадлежащая прямой m. Найдем точку А1, симметричную А относительно прямой m. Проведем перпендикуляр из точки А к прямой m, продолжим его по другую сторону прямой. С помощью линейки или циркуля измерим расстояние от точки А до прямой m и отложим на продолжении перпендикуляра такое же расстояние от точки его пересечения с прямой, отметим точку А1. Точка А1 будет симметрична точке А относительно прямой m. Две точки А и А1 называются симметричными относительно прямой m, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая m – ось симметрии. Каждая точка оси симметрии симметрична сама себе.
Построим геометрическую фигуру симметричную данной относительно прямой. Для этого необходимо найти точки симметричные вершинам данной фигуры относительно этой прямой и потом соединить эти точки отрезками.
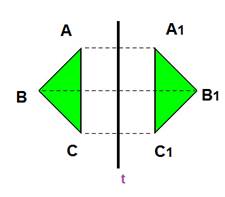
Например, построим треугольник А1В1С1 симметричный треугольнику АВС относительно оси t. Из вершин треугольника АВС проведем перпендикуляры к прямой t. Отложим расстояния от вершин треугольника до прямой t по другую сторону от оси по перпендикулярным прямым, полученные точки соединим. Получится треугольник А1В1С1 симметричный треугольнику АВС. При сгибании плоскости чертежа по оси симметрии (прямой t) симметричные фигуры (треугольники) совместятся.
Симметричными могут быть не только две фигуры, но и части одной фигуры. Так в некоторых фигурах можно провести ось симметрии. Говорят, что такие фигуры имеют осевую симметрию. Осевой симметрией обладают равнобедренные треугольники, у прямоугольников – две оси симметрии, у квадрата – четыре, а у круга – множество осей симметрии.
Геометрические тела тоже могут иметь ось симметрии: цилиндр, параллелепипед, конус.
Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Симметрично практически все: транспортные средства, предметы домашнего обихода (мебель, посуда), некоторые музыкальные инструменты.

Законы природы, которые управляют картиной явлений, также подчиняются принципам симметрии. Основу красоты многих форм, созданных природой, составляет симметрия. Симметричны листья дерева, цветы, колосья пшеницы, снежинки. Осевую симметрию имеет внешнее строение тела животных. И красота человеческого тела обусловлена пропорциональностью и симметрией.

Нагляднее всего симметрия видна в архитектуре. В сознании архитекторов она стала олицетворением закономерности, целесообразности, красоты. Пирамида Хеопса в Египте, Собор Парижской Богоматери и Эйфелева башня во Франции, Биг Бен в Великобритании.
Архитектура русских православных храмов и соборов также говорит о том, что с древнейших времен архитекторы хорошо знали математическую пропорцию и симметрию и использовали их при строительстве архитектурных сооружений: Кремль в Москве, Казанский и Исаакиевский соборы в Санкт-Петербурге.
Таким образом, на этом уроке мы познакомились с понятием осевая симметрия, научились строить фигуры симметричные относительно оси, узнали о роли симметрии в повседневной жизни.
Домашняя работа
Стр. 149 — 151
Упр. 576 — 581
Сделайте в тетради, проверка будет по выходу из карантина