Материалы урока
Вспомним, как в курсе геометрии были введены синус, косинус и тангенс угла из промежутка от 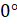 до
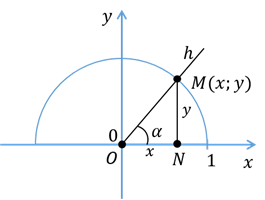
до 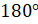 . На координатной плоскости построим полуокружность с центром в начале координат и единичным радиусом, расположенную в первой и второй четвертях. Такую полуокружность называют единичной полуокружностью.
. На координатной плоскости построим полуокружность с центром в начале координат и единичным радиусом, расположенную в первой и второй четвертях. Такую полуокружность называют единичной полуокружностью.
Затем из точки 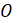 проведём луч
проведём луч 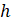 , который пересекает нашу полуокружность в точке
, который пересекает нашу полуокружность в точке 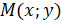 . Угол между лучом
. Угол между лучом 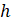 и положительным направлением оси
и положительным направлением оси 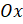 обозначим
обозначим 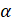 . При этом, если луч
. При этом, если луч 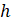 совпадает с положительным направлением оси
совпадает с положительным направлением оси 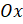 , то считают, что угол
, то считают, что угол 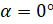 .
.
Пусть угол 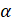 острый. Опустим из точки
острый. Опустим из точки 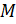 перпендикуляр
перпендикуляр 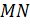 на ось
на ось 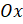 и получим прямоугольный треугольник
и получим прямоугольный треугольник 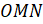 . Тогда из этого треугольника имеем:
. Тогда из этого треугольника имеем: 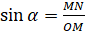 ;
; 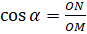 .
. 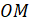 – это радиус единичной полуокружности, а значит, равняется
– это радиус единичной полуокружности, а значит, равняется 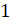 .
. 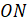 равняется абсциссе точки
равняется абсциссе точки 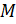 , то есть
, то есть 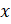 .
. 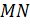 равняется ординате точки
равняется ординате точки 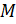 , то есть
, то есть 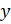 . Подставим эти значения в выражения синуса и косинуса и получим, что
. Подставим эти значения в выражения синуса и косинуса и получим, что 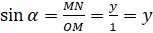 ,
, 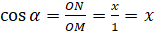 .
.
А если угол 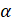 не является острым, то как определяются синус и косинус этого угла?
не является острым, то как определяются синус и косинус этого угла?
Если угол альфа прямой, тупой, развёрнутый или равен нулю, то синус и косинус также определяются по формулам: 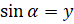 ,
, 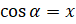 .
.
Таким образом, для любого угла альфа из промежутка от 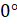 до
до 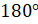 синусом угла
синусом угла 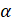 называется ордината точки
называется ордината точки 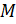 , а косинусом угла
, а косинусом угла 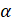 – абсцисса точки
– абсцисса точки 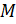 .
.
При этом не забудем отметить, что так как координаты 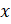 и
и 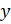 точек единичной полуокружности удовлетворяют неравенствам
точек единичной полуокружности удовлетворяют неравенствам 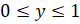 , а
, а 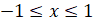 , то для
, то для 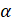 из промежутка от
из промежутка от 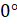 до
до 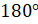 справедливы неравенства
справедливы неравенства 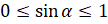 ;
; 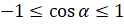 .
.
Тангенсом угла 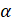 , причём
, причём 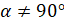 , называется отношение
, называется отношение 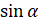 к
к 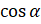 :
: 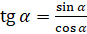 . Отметим, что
. Отметим, что 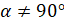 , так как
, так как 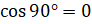 , а в формуле знаменатель не должен обращаться в нуль.
, а в формуле знаменатель не должен обращаться в нуль.
Так как же определяются синус, косинус и тангенс произвольного угла?
Запомните! Синусом угла 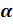 называется ордината точки
называется ордината точки 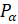 , полученной поворотом точки
, полученной поворотом точки 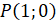 вокруг начала координат на угол
вокруг начала координат на угол 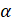 . Обозначают:
. Обозначают: 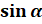 .
.
Косинусом угла 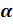 называется абсцисса точки
называется абсцисса точки 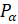 , полученной поворотом точки
, полученной поворотом точки 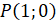 вокруг начала координат на угол
вокруг начала координат на угол 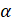 . Обозначают:
. Обозначают: 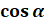 .
.
Причём угол 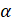 может выражаться и в градусах, и в радианах.
может выражаться и в градусах, и в радианах.
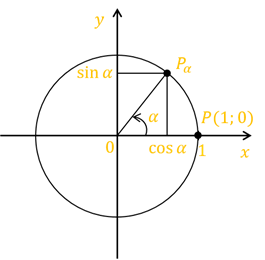
Давайте найдём значения синуса и косинуса угла 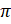 , то есть угла
, то есть угла 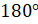 . При повороте точки
. При повороте точки 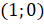 на угол
на угол 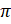 получаем точку
получаем точку 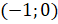 . Ордината полученной точки равна
. Ордината полученной точки равна 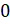 , а, следовательно,
, а, следовательно, 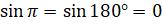 . Абсцисса полученной точки равна
. Абсцисса полученной точки равна 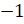 , а, следовательно,
, а, следовательно, 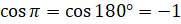 .
.
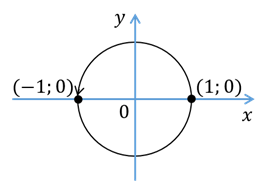
Отметим, что приведённые выше определения синуса и косинуса произвольного угла в случае, если угол принадлежит промежутку от 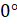 до
до 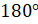 , совпадают с определениями синуса и косинуса из курса геометрии, которые мы с вами повторили в начале урока. Так, например,
, совпадают с определениями синуса и косинуса из курса геометрии, которые мы с вами повторили в начале урока. Так, например, 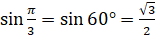 ,
, 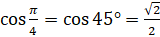 .
.
А давайте найдём значения синуса и косинуса угла не из промежутка от 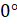 до
до 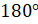 .
.
Найдём 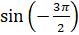 и
и 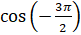 . Итак, при повороте точки
. Итак, при повороте точки 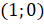 на угол
на угол 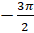 мы осуществим поворот по часовой стрелке и окажемся в точке
мы осуществим поворот по часовой стрелке и окажемся в точке 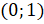 . Ордината полученной точки равна
. Ордината полученной точки равна 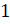 , следовательно, с
, следовательно, с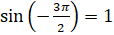 . Абсцисса полученной точки равна
. Абсцисса полученной точки равна 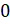 , следовательно,
, следовательно, 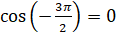 .
.
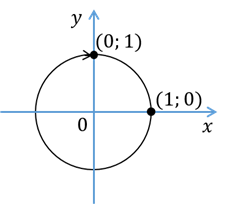
Сейчас давайте решим уравнение 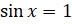 . Решить это уравнение означает найти все углы, синус которых равен
. Решить это уравнение означает найти все углы, синус которых равен 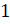 . Ординату, равную
. Ординату, равную 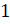 , имеет точка единичной окружности
, имеет точка единичной окружности 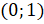 . Эта точка получается из точки
. Эта точка получается из точки 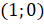 поворотом на угол
поворотом на угол  , на угол
, на угол 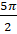 , на угол
, на угол 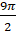 и так далее. А также на угол
и так далее. А также на угол 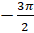 , на угол
, на угол 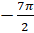 и так далее.
и так далее.
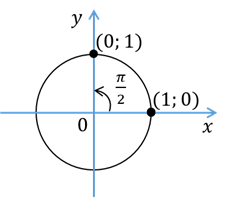
При этом 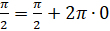 ,
, 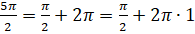 ,
, 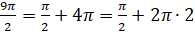 ,
,
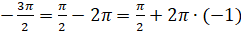 ,
, 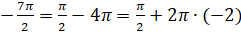 .
.
Следовательно, 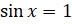 при
при 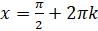 , где
, где 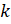 – это любое целое число.
– это любое целое число.
Вы знаете, что множество целых чисел обозначается буквой 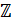 . Обозначить то, что число
. Обозначить то, что число 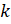 принадлежит целым числам можно вот таким образом:
принадлежит целым числам можно вот таким образом: 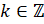 . Читают:
. Читают: 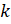 принадлежит
принадлежит 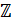 . Тогда ответ к нашей задаче можно записать так:
. Тогда ответ к нашей задаче можно записать так: 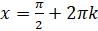 ,
, 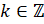 .
.
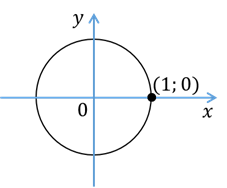
Решим уравнение 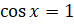 . Абсциссу, равную
. Абсциссу, равную 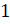 , имеет точка
, имеет точка 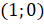 . Эта точка получается из точки
. Эта точка получается из точки 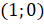 поворотом на
поворотом на 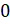 рад, то есть точка остаётся на своём месте; на угол
рад, то есть точка остаётся на своём месте; на угол 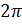 , на угол
, на угол 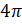 и так далее. А также на угол
и так далее. А также на угол 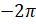 ,
, 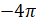 и так далее.
и так далее.
При этом 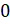 рад мы можем записать как
рад мы можем записать как 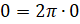 ,
, 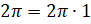 ,
, 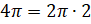 ,
, 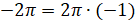 ,
, 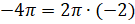 .
.
Следовательно, 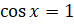 при
при 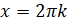 ,
, 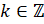 .
.
А что называют тангенсом произвольного угла?
Запомните! Тангенсом угла 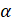 называется отношение синуса угла
называется отношение синуса угла 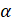 к его косинусу. Обозначают:
к его косинусу. Обозначают: 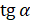 .
.
Таким образом, можем записать, что 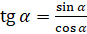 .
.
Иногда используют котангенс угла 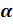 , который равен отношению косинуса угла
, который равен отношению косинуса угла 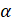 к синусу угла
к синусу угла 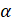 :
: 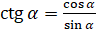 . При этом
. При этом 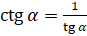 .
.
Давайте найдём 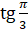 и
и 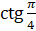 .
.
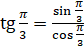 . Подставим значения синуса и косинуса:
. Подставим значения синуса и косинуса: 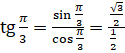 . Выполним вычисления и в результате получим
. Выполним вычисления и в результате получим 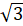 .
.
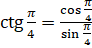 . Подставим значения косинуса и синуса:
. Подставим значения косинуса и синуса: 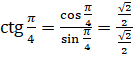 . Выполним вычисления и получим
. Выполним вычисления и получим 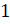 .
.
Также 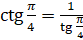 .
. 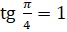 , а, следовательно,
, а, следовательно, 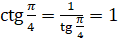 .
.
Важно помнить, что 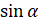 и
и 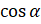 определены для любого угла
определены для любого угла 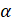 , а их значения заключены в промежутках от
, а их значения заключены в промежутках от 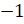 до
до 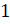 , так как координаты точек единичной окружности заключены в промежутках от
, так как координаты точек единичной окружности заключены в промежутках от 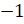 до
до 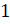 .
.
А вот 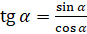 определён только для тех углов, для которых
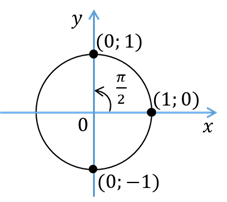
определён только для тех углов, для которых 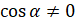 , так как делить на нуль нельзя. Найдём углы, косинус которых равен нулю. Итак, абсциссу, равную
, так как делить на нуль нельзя. Найдём углы, косинус которых равен нулю. Итак, абсциссу, равную 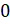 , имеет точка
, имеет точка 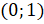 и
и 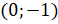 . Эти точки получаются поворотом точки
. Эти точки получаются поворотом точки 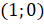 на углы
на углы  ,
, 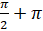 ,
, 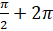 и так далее. А также на углы
и так далее. А также на углы 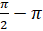 ,
, 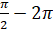 и так далее.
и так далее.
Следовательно, 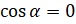 при
при 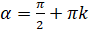 ,
, 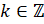 .
.
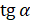 определён для любых углов, кроме
определён для любых углов, кроме 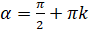 ,
, 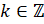 .
.
А для каких углов определён 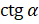 ?
? 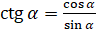 определён только для тех углов, для которых
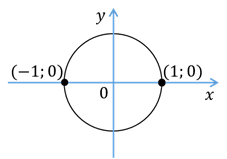
определён только для тех углов, для которых 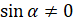 . Найдём углы, синус которых равен нулю. Итак, ординату, равную нулю, имеет точка
. Найдём углы, синус которых равен нулю. Итак, ординату, равную нулю, имеет точка 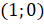 и точка
и точка 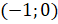 . Эти точки получаются поворотом точки
. Эти точки получаются поворотом точки 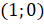 на углы
на углы 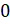 ,
, 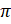 ,
, 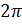 ,
, 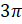 и так далее. А также на углы
и так далее. А также на углы 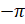 ,
, 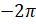 ,
, 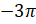 и так далее.
и так далее.
Следовательно, 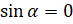 при
при 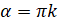 ,
, 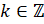 .
.
Тогда 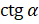 определён для любых углов, кроме
определён для любых углов, кроме 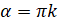 ,
, 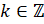 .
.
На следующем слайде приведена таблица значений синуса, косинуса, тангенса и котангенса, с которыми вы будете встречаться чаще всего:
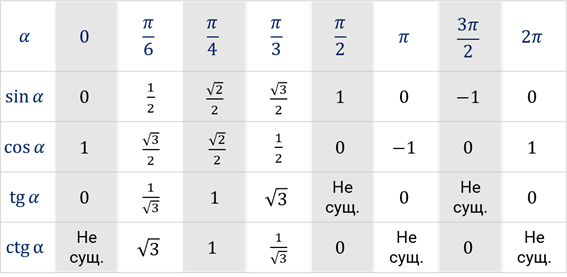
Найдём значение выражения 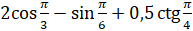 .
.
Воспользуемся только что приведённой таблицей. Подставим значения в наше выражения: 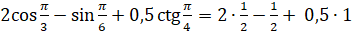 . Теперь выполним вычисления и в результате получим
. Теперь выполним вычисления и в результате получим 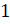 .
.
Отметим, что значения синуса, косинуса, тангенса и котангенса для углов, которых нет в этой таблице, можно найти с помощью инженерного микрокалькулятора или по четырёхзначным математическим таблицам Брадиса.