Материалы урока
Прежде, чем приступить к рассмотрению новой темы вспомним, что каждой точке прямой ставится в соответствие некоторая точка окружности.
Также вспомним, что центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.
Вспомним формулу перехода от радианной меры к градусной 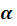 рад
рад 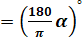 и формулу перехода от градусной меры к радианной
и формулу перехода от градусной меры к радианной 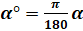 рад.
рад.
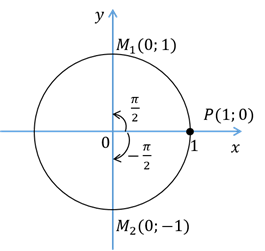
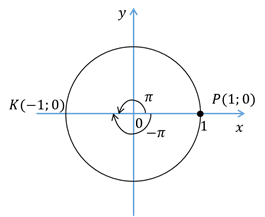
А теперь на координатной плоскости рассмотрим окружность единичного радиуса с центром в начале координат. Такую окружность называют единичной окружностью.
Введём понятие поворота точки единичной окружности вокруг начала координат на угол 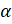 рад, где
рад, где 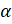 – это любое действительное число. Отметим точку
– это любое действительное число. Отметим точку 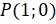 . Эта точка расположена на окружности.
. Эта точка расположена на окружности.
Пусть 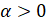 . Представим, что точка, двигаясь по единичной окружности от точки
. Представим, что точка, двигаясь по единичной окружности от точки 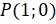 против часовой стрелки, прошла путь длиной
против часовой стрелки, прошла путь длиной 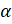 . Конечную точку пути обозначим
. Конечную точку пути обозначим 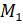 .
.
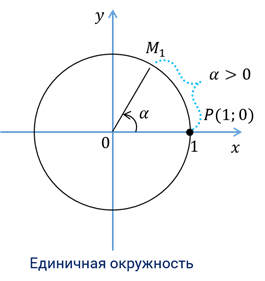
В таком случае будем говорить, что точка 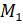 получена из точки
получена из точки 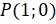 путём поворота на угол
путём поворота на угол 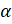 рад вокруг начала координат.
рад вокруг начала координат.
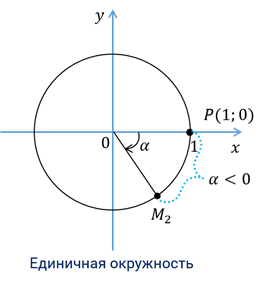
Теперь пусть 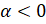 . В этом случае поворот на угол
. В этом случае поворот на угол 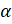 рад будем совершать по часовой стрелке. Точка пройдёт путь длиной модуль
рад будем совершать по часовой стрелке. Точка пройдёт путь длиной модуль 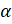 . Конечную точку пути обозначим
. Конечную точку пути обозначим 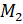 .
.
Если же 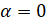 , то точка остаётся на месте.
, то точка остаётся на месте.
Давайте рассмотрим некоторые примеры поворотов точки 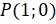 на некоторый угол.
на некоторый угол.
Итак, при повороте точки 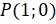 на угол
на угол  рад мы совершаем движение против часовой стрелки и получаем точку
рад мы совершаем движение против часовой стрелки и получаем точку 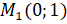 .
.
А при повороте точки 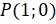 на угол
на угол 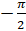 рад мы двигаемся по часовой стрелке и получаем точку
рад мы двигаемся по часовой стрелке и получаем точку 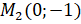 .
.
При повороте точки 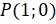 на угол
на угол 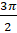 рад мы осуществим поворот против часовой стрелки на
рад мы осуществим поворот против часовой стрелки на  рад трижды и окажемся в точке
рад трижды и окажемся в точке 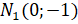 .
.
При повороте точки 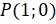 на угол
на угол 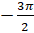 рад мы осуществим поворот по часовой стрелке на
рад мы осуществим поворот по часовой стрелке на 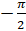 рад трижды и окажемся в точке
рад трижды и окажемся в точке 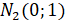 .
.
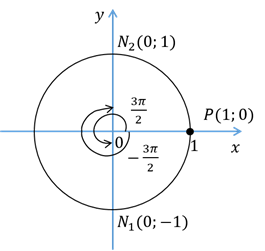
При повороте точки 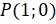 на угол
на угол 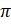 рад мы осуществим поворот по часовой стрелке и окажемся в точке
рад мы осуществим поворот по часовой стрелке и окажемся в точке 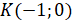 .
.
При повороте точки 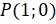 на угол
на угол 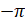 рад мы осуществим поворот против часовой стрелки и снова окажемся в точке
рад мы осуществим поворот против часовой стрелки и снова окажемся в точке 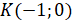 .
.
Ранее в курсе геометрии вы рассматривали углы от 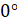 до
до 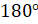 . Теперь, используя поворот точки единичной окружности вокруг начала координат, можно рассматривать углы, которые больше
. Теперь, используя поворот точки единичной окружности вокруг начала координат, можно рассматривать углы, которые больше 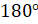 , а также отрицательные углы.
, а также отрицательные углы.
А задавать угол поворота надо в градусах или радианах? Угол поворота можно задавать и в градусах, и в радианах. Так, например, поворот точки 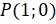 на угол
на угол  означает то же, что и поворот на
означает то же, что и поворот на 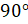 . А поворот на
. А поворот на 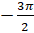 – это поворот на
– это поворот на 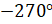 .
.
Далее приведена таблица поворотов на наиболее часто встречающиеся углы, выраженные в радианной и градусной мере:
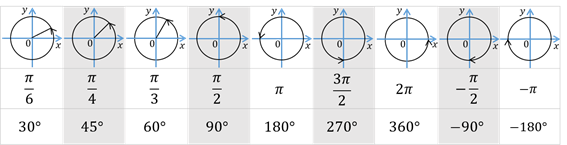
Обратите внимание, что при повороте на 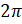 , то есть на
, то есть на 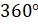 , точка возвращается в своё первоначальное положение.
, точка возвращается в своё первоначальное положение.
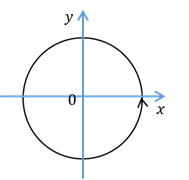
А где окажется точка при повороте на 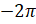 ? При повороте на
? При повороте на 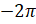 , то есть на
, то есть на 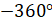 , точка также вернётся в своё первоначальное положение.
, точка также вернётся в своё первоначальное положение.
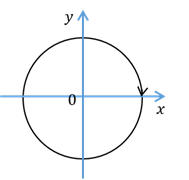
Давайте рассмотрим пример поворота на угол, который больше 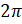 . Например, на угол
. Например, на угол 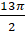 . Представим
. Представим 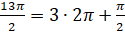 . Получается, что при повороте на этот угол точка
. Получается, что при повороте на этот угол точка 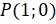 совершает три полных оборота против часовой стрелки и ещё проходит путь
совершает три полных оборота против часовой стрелки и ещё проходит путь  .
.
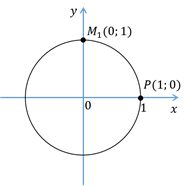
Теперь рассмотрим пример поворота на угол  , то есть на угол меньший
, то есть на угол меньший 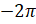 . Представим
. Представим 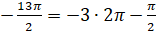 . В этом случае точка совершает три полных оборота по часовой стрелке и ещё проходит путь
. В этом случае точка совершает три полных оборота по часовой стрелке и ещё проходит путь  в этом же направлении.
в этом же направлении.
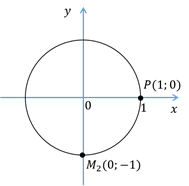
Получается, что при повороте точки 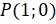 на угол
на угол 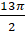 получаем ту же точку, что и при повороте на угол
получаем ту же точку, что и при повороте на угол  , а при повороте точки
, а при повороте точки 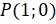 на угол
на угол  получаем ту же точку, что и при повороте на угол
получаем ту же точку, что и при повороте на угол 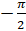 .
.
Вообще, если угол 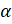 можно представить как
можно представить как 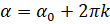 , где
, где 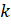 – целое число, то при повороте на угол
– целое число, то при повороте на угол 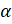 получаем ту же самую точку, что и при повороте на угол
получаем ту же самую точку, что и при повороте на угол 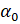 .
.
Таким образом, можем сделать вывод, что каждому действительному числу 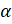 соответствует единственная точка единичной окружности, получаемая поворотом точки
соответствует единственная точка единичной окружности, получаемая поворотом точки 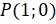 на угол
на угол 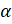 рад.
рад.
Однако одной и той же точке 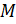 единичной окружности соответствует бесконечное множество действительных чисел
единичной окружности соответствует бесконечное множество действительных чисел 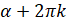 , где
, где 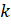 – целое число, задающих поворот точки
– целое число, задающих поворот точки 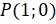 в точку
в точку 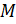 .
.
Найдём координаты точки, полученной поворотом точки 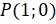 на угол
на угол 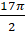 . Представим
. Представим 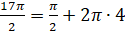 . Тогда при повороте точки на угол
. Тогда при повороте точки на угол 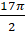 мы получим ту же самую точку, что и при повороте на угол
мы получим ту же самую точку, что и при повороте на угол  , то есть точку с координатами
, то есть точку с координатами 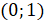 .
.
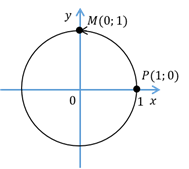
Найдём координаты точки, полученной поворотом точки 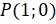 на угол
на угол 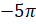 . Представим
. Представим 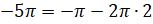 . Тогда при повороте на
. Тогда при повороте на 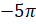 мы получаем ту же самую точку, что и при повороте на
мы получаем ту же самую точку, что и при повороте на 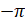 , то есть точку с координатами
, то есть точку с координатами 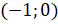 .
.
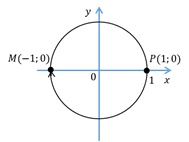
И найдём координаты точки, полученной поворотом точки 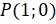 на угол
на угол  .
.
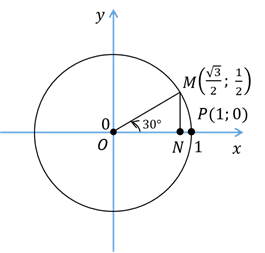
Для этого выполним поворот точки против часовой стрелки на угол  , то есть на
, то есть на 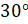 , и получим точку
, и получим точку 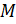 . Опустим из неё перпендикуляр
. Опустим из неё перпендикуляр 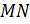 на ось
на ось 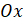 и рассмотрим прямоугольный треугольник
и рассмотрим прямоугольный треугольник 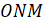 . Так как координаты точки
. Так как координаты точки 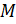 численно равны длинам катетов этого треугольника, то нам остаётся найти длины
численно равны длинам катетов этого треугольника, то нам остаётся найти длины 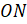 и
и 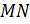 .
.
Гипотенузой этого треугольника является отрезок 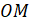 . Причём
. Причём 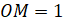 , так как это радиус нашей единичной окружности. Угол
, так как это радиус нашей единичной окружности. Угол 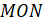 равен
равен 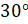 , так как мы осуществляли поворот на
, так как мы осуществляли поворот на  , то есть на
, то есть на 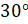 .
.
А мы ведь знаем из геометрии, что катет прямоугольного треугольника, лежащий против угла в 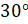 , равен половине гипотенузы. Значит, катет
, равен половине гипотенузы. Значит, катет 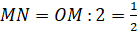 .
.
Теперь вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (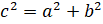 ). Запишем её для нашего треугольника:
). Запишем её для нашего треугольника: 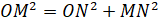 . Выразим неизвестный нам катет
. Выразим неизвестный нам катет 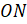 :
: 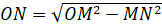 . Подставим значения
. Подставим значения 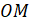 и
и 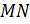 :
: 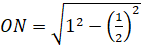 . Выполним вычисления и в результате получим
. Выполним вычисления и в результате получим 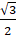 .
.
Таким образом, можем записать, что точка 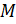 имеет абсциссу, равную длине катета
имеет абсциссу, равную длине катета 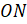 , то есть
, то есть 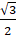 , и ординату, равную длине катета
, и ординату, равную длине катета 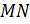 , то есть
, то есть  .
.
А сейчас давайте выполним несколько заданий.
Задание первое. Найти координаты точки, полученной поворотом точки 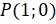 на угол а)
на угол а) 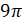 ; б)
; б) 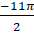 ; в)
; в) 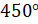 .
.
Решение.
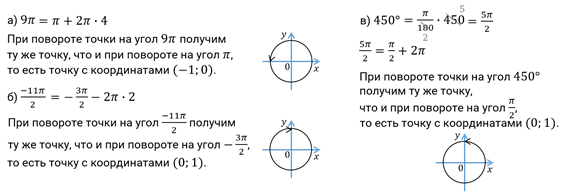
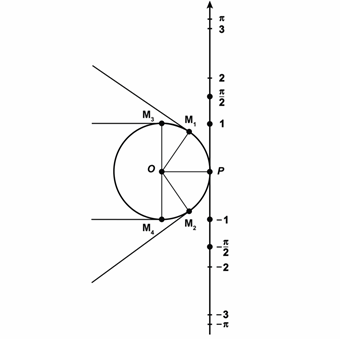
И решим ещё одно задание. Найдите число 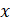 , где
, где 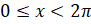 , и натуральное число
, и натуральное число 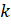 , такие, чтобы выполнялось равенство
, такие, чтобы выполнялось равенство 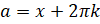 , если а)
, если а) 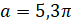 ; б)
; б) 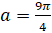 .
.
Решение.