Когда корень только один
Если квадратный трёхчлен имеет только один корень, то формула разложения квадратного трёхчлена примет такой вид:
ax2 + bx + c = a(x − x1)2
Вместо x1 подставляется единственный найденный корень квадратного трёхчлена.
Например, квадратный трёхчлен x2 − 6x + 9 имеет только один корень. Дискриминант этого квадратного трёхчлена равен нулю:
D = b2 − 4ac = (−6)2 − 4 × 1 × 9 = 36 − 36 = 0
и далее вычисляется единственный корень по известной формуле:
![]()
Тогда по формуле, которая приведена выше, получим:
ax2 + bx + c = a(x − x1)2
x2 − 6x + 9 = (x − 3)2
Внимательные наверное сразу поняли почему происходит именно так. Если дискриминант квадратного трёхчлена равен нулю, то корень вычисляется по формуле:
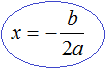
Но никто не запрещает нам использовать формулы вычисления корней квадратного трёхчлена:


Просто в этом случае мы получим один и тот же корень 3
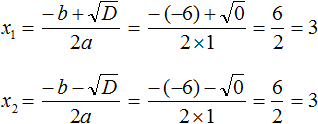
Видим, что x1 = x2. Теперь для квадратного трёхчлена x2 − 6x + 9 применим нашу формулу разложения, которую мы применяем когда два корня:
x2 − 6x + 9 = (x − 3)(x − 3)
Выражение (x − 3)(x − 3) это перемножение двух сомножителей, каждый из которых равен (x − 3). Это выражение можно заменить на выражение (x − 3)2
x2 − 6x + 9 = (x − 3)2