Прежде, чем мы приступим к изучению новой темы, давайте вспомним, что тригонометрическим уравнением называется уравнение, которое содержит переменную под знаком тригонометрических функций. Уравнения вида: 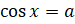 ,
, 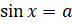 ,
, 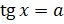 и
и 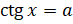 , где
, где 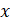 – переменная, а число
– переменная, а число 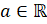 , называются простейшими тригонометрическими уравнениями. Также мы вспомним, что все корни уравнения
, называются простейшими тригонометрическими уравнениями. Также мы вспомним, что все корни уравнения 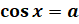 , где
, где 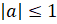 , можно найти по формуле:
, можно найти по формуле: 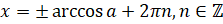 . Все корни уравнения
. Все корни уравнения 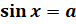 , где
, где 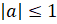 , можно найти по формуле:
, можно найти по формуле: 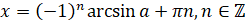 . Все корни уравнения
. Все корни уравнения 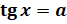 , где
, где 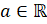 , можно найти по формуле:
, можно найти по формуле: 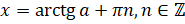 . А все корни уравнения
. А все корни уравнения 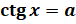 , где
, где 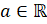 , можно найти по формуле:
, можно найти по формуле: 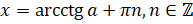 .
.
На этом уроке мы с вами рассмотрим примеры решения тригонометрических уравнений, которые различными способами сводятся к решению простейших тригонометрических уравнений.
Итак, уравнения, сводящиеся к квадратным.
Решим уравнение: 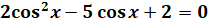 . Это уравнение является квадратным относительно
. Это уравнение является квадратным относительно 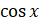 . Обозначим
. Обозначим 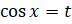 . Тогда исходное уравнение примет вид:
. Тогда исходное уравнение примет вид: 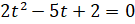 . Решим это квадратное уравнение:
. Решим это квадратное уравнение: 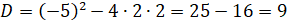 . Его корнями являются
. Его корнями являются 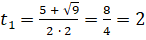 и
и 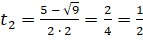 . Теперь вернёмся к замене и получим два простейших уравнения:
. Теперь вернёмся к замене и получим два простейших уравнения: 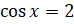 и
и 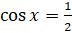 . Первое уравнение не имеет решений, так как
. Первое уравнение не имеет решений, так как 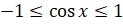 . По формуле нахождения корней уравнения
. По формуле нахождения корней уравнения 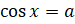 решением второго уравнения будет
решением второго уравнения будет 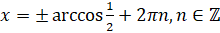 . Так как
. Так как 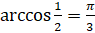 , то
, то 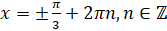 . Ответ:
. Ответ: 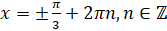 .
.
Рассмотрим уравнение вида 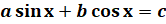 .
.
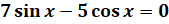 . Разделим обе части этого уравнения на
. Разделим обе части этого уравнения на 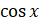 и получим:
и получим: 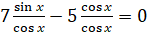 ,
, 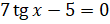 .
.
Перенесём 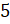 в правую часть уравнения и разделим обе части уравнения на
в правую часть уравнения и разделим обе части уравнения на 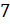 :
:  . Получили простейшее тригонометрическое уравнение. По формуле нахождения корней уравнения
. Получили простейшее тригонометрическое уравнение. По формуле нахождения корней уравнения 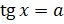 его решением будет
его решением будет 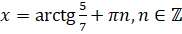 . Ответ:
. Ответ: 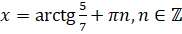 .
.
Обратите внимание, что при решении обе части исходного уравнения были поделены на 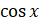 . А при делении уравнения на выражение, которое содержит неизвестное, могут быть потеряны корни. Следовательно, необходимо проверить, не являются ли корни уравнения
. А при делении уравнения на выражение, которое содержит неизвестное, могут быть потеряны корни. Следовательно, необходимо проверить, не являются ли корни уравнения 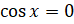 корнями нашего уравнения. Если
корнями нашего уравнения. Если 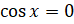 , то из нашего уравнения
, то из нашего уравнения 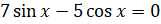 следует, что и
следует, что и 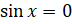 . А из основного тригонометрического тождества
. А из основного тригонометрического тождества 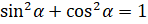 следует, что
следует, что 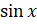 и
и 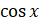 не могут одновременно равняться нулю. Таким образом, при делении уравнения вида:
не могут одновременно равняться нулю. Таким образом, при делении уравнения вида: 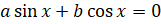 , где
, где 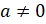 ,
, 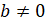 (а значит, и данного уравнения),
(а значит, и данного уравнения), 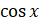 или на
или на 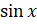 получаем уравнение, которое равносильно данному.
получаем уравнение, которое равносильно данному.
И давайте решим уравнение: 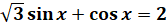 . Применим формулы
. Применим формулы 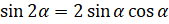 ,
, 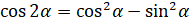 к левой части уравнения, правую часть уравнения запишем как произведение
к левой части уравнения, правую часть уравнения запишем как произведение 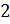 и
и 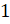 , тогда уравнение примет вид:
, тогда уравнение примет вид: 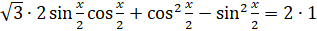 . Затем
. Затем 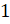 по основному тригонометрическому тождеству запишем как
по основному тригонометрическому тождеству запишем как 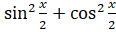 :
: 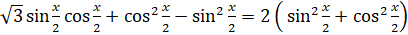 . Раскроем скобки, перенесём слагаемые из правой части уравнения в левую, приведём подобные слагаемые:
. Раскроем скобки, перенесём слагаемые из правой части уравнения в левую, приведём подобные слагаемые: 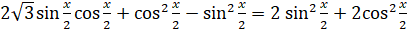 ,
, 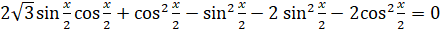 ,
, 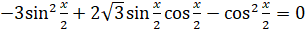 . Теперь разделим это уравнение на
. Теперь разделим это уравнение на 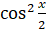 и получим равносильное уравнение:
и получим равносильное уравнение: 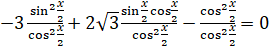 ,
, 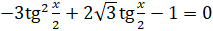 . Обозначим
. Обозначим 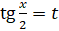 . Тогда исходное уравнение примет вид
. Тогда исходное уравнение примет вид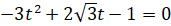 . Решим это квадратное уравнение:
. Решим это квадратное уравнение: 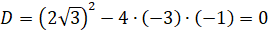 . Его корнем будет
. Его корнем будет 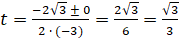 . Теперь вернёмся к замене и получим простейшее уравнение:
. Теперь вернёмся к замене и получим простейшее уравнение: 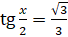 . По формуле нахождения корней уравнения
. По формуле нахождения корней уравнения 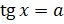 можем записать, что
можем записать, что 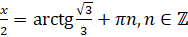 . Так как
. Так как 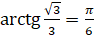 , то
, то 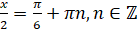 . Тогда
. Тогда 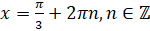 . Ответ:
. Ответ: 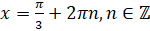 .
.
Таким образом, мы с вами решили уравнение вида: 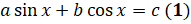 , где где
, где где 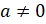 ,
, 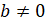 ,
, 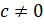 . Такое уравнение можно решить с помощью введения вспомогательного угла. Давайте выясним, в чём заключается метод введения вспомогательного угла. В первую очередь необходимо проверить, выполняется ли условие
. Такое уравнение можно решить с помощью введения вспомогательного угла. Давайте выясним, в чём заключается метод введения вспомогательного угла. В первую очередь необходимо проверить, выполняется ли условие 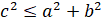 . Если условие выполняется, то разделим обе части уравнения на
. Если условие выполняется, то разделим обе части уравнения на 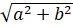 :
: 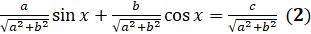 .
.
Легко убедиться, что коэффициенты 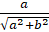 и
и 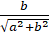 связаны равенством:
связаны равенством: 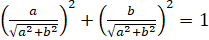 . Исходя из основного тригонометрического тождества
. Исходя из основного тригонометрического тождества 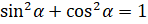 : обозначим
: обозначим 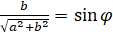 ,
, 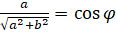 . Таким образом, уравнение
. Таким образом, уравнение 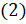 можно записать в виде:
можно записать в виде: 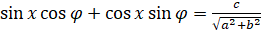 . Теперь, применив к левой части уравнения формулу
. Теперь, применив к левой части уравнения формулу 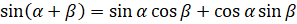 , получим
, получим 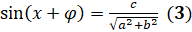 .
.
Таким образом, уравнение 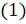 мы свели к простейшему тригонометрическому уравнению.
мы свели к простейшему тригонометрическому уравнению.
Итак, решим предыдущее уравнение 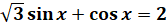 введением вспомогательного угла. Здесь у нас
введением вспомогательного угла. Здесь у нас 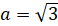 ,
, 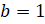 ,
, 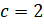 . Проверим, выполняется ли условие
. Проверим, выполняется ли условие 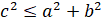 . Подставим значения
. Подставим значения 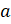 ,
, 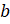 и
и 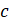 :
: 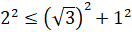 ,
, 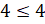 . Видим, что получили верное неравенство, а значит, условие выполняется.
. Видим, что получили верное неравенство, а значит, условие выполняется. 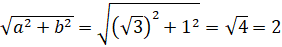 . Разделим обе части нашего уравнения на
. Разделим обе части нашего уравнения на 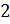 :
: 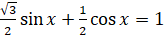 . Теперь введём вспомогательный аргумент
. Теперь введём вспомогательный аргумент 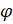 , такой, что
, такой, что 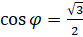 ,
, 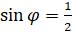 .
. 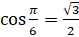 ,
, 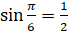 , тогда наше уравнение примет вид:
, тогда наше уравнение примет вид: 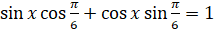 . По формуле
. По формуле 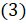 запишем:
запишем: 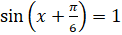 . Мы знаем, что корни уравнения
. Мы знаем, что корни уравнения 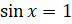 находятся по формуле
находятся по формуле 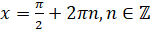 . Тогда в нашем случае
. Тогда в нашем случае 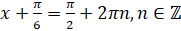 . Перенесём
. Перенесём  в правую часть:
в правую часть: 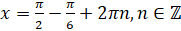 . Вычтем
. Вычтем  из
из  и получим, что
и получим, что 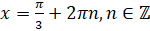 . Ответ:
. Ответ: 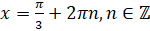 .
.
Тригонометрические уравнения, правая часть которых равна нулю, часто решаются разложением левой части на множители. Решим уравнение: 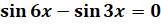 . Воспользуемся формулой
. Воспользуемся формулой 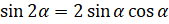 и запишем
и запишем 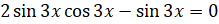 . Вынесем
. Вынесем 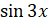 :
: 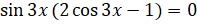 . Произведение обращается в нуль, если один из множителей равен нулю. Следовательно,
. Произведение обращается в нуль, если один из множителей равен нулю. Следовательно, 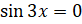 или
или 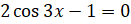 . Решим уравнение
. Решим уравнение 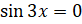 . Мы знаем, что корни уравнения
. Мы знаем, что корни уравнения 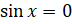 находятся по формуле
находятся по формуле 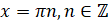 . Тогда в нашем случае
. Тогда в нашем случае 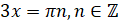 . Откуда
. Откуда 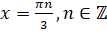 . Решим уравнение
. Решим уравнение 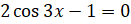 . Перенесём
. Перенесём 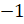 в правую часть уравнения и разделим обе части уравнения на
в правую часть уравнения и разделим обе части уравнения на 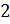 :
: 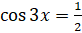 . По формуле нахождения корней уравнения
. По формуле нахождения корней уравнения 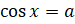 получаем:
получаем: 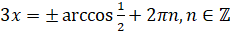 . Так как
. Так как 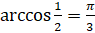 , то
, то 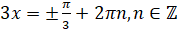 . Тогда
. Тогда 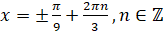 . Ответ:
. Ответ: 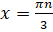 ,
, 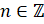 ,
, 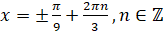 .
.
Есть уравнения, которые можно решить с помощью формул половинного угла. Решим уравнение: 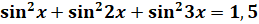 . Применим формулу
. Применим формулу 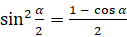 и запишем первое слагаемое в левой части как
и запишем первое слагаемое в левой части как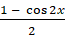 , второе слагаемое запишем как
, второе слагаемое запишем как 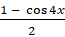 , третье слагаемое запишем как
, третье слагаемое запишем как 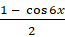 ,
, 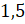 в правой части уравнения запишем как
в правой части уравнения запишем как  :
: 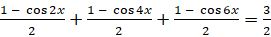 . Умножим обе части уравнения на
. Умножим обе части уравнения на 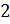 :
: 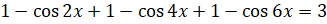 . Сложим единицы в левой части:
. Сложим единицы в левой части: 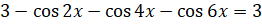 . Перенесём
. Перенесём 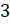 в правую часть:
в правую часть: 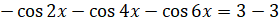 ,
, 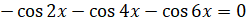 . Умножим уравнение на
. Умножим уравнение на 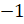 :
: 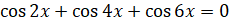 . Поменяем местами первое и второе слагаемые:
. Поменяем местами первое и второе слагаемые: 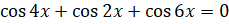 . Теперь применим ко второму и третьему слагаемым формулу
. Теперь применим ко второму и третьему слагаемым формулу 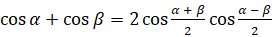 :
: 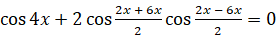 ,
, 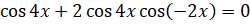 ,
, 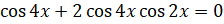 . Вынесем за скобки
. Вынесем за скобки 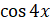 :
: 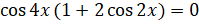 . Произведение обращается в нуль, если один из множителей равен нулю. Следовательно,
. Произведение обращается в нуль, если один из множителей равен нулю. Следовательно, 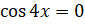 или
или 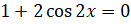 . Решим уравнение
. Решим уравнение 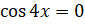 . Корни уравнения
. Корни уравнения 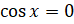 находятся по формуле
находятся по формуле 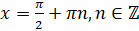 . Тогда для нашего уравнения
. Тогда для нашего уравнения 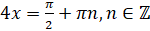 . Откуда
. Откуда 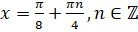 .
.
Решим уравнение 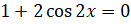 . Перенесём
. Перенесём 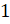 в правую часть уравнения и разделим обе части уравнения на
в правую часть уравнения и разделим обе части уравнения на 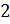 :
: 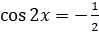 . По формуле нахождения корней уравнения
. По формуле нахождения корней уравнения 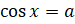 получаем
получаем 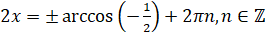 .
. 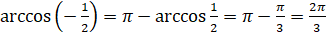 . Тогда
. Тогда 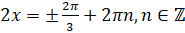 . Отсюда
. Отсюда 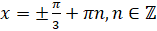 . Ответ:
. Ответ: 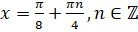 ,
, 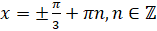 .
.