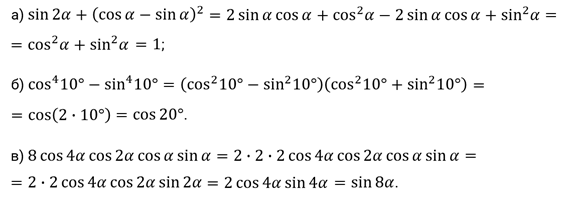Вспомним формулы сложения для синуса: 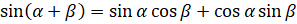 ,
, 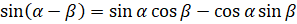 ; косинуса:
; косинуса: 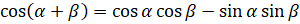 ,
, 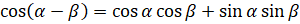 ; тангенса:
; тангенса: 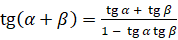 ;
; 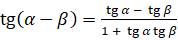 . Используя эти формулы, мы с вами выведем формулы синуса, косинуса и тангенса двойного угла.
. Используя эти формулы, мы с вами выведем формулы синуса, косинуса и тангенса двойного угла.
Итак, в формулу 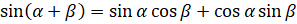 вместо
вместо 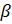 подставим
подставим 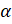 :
: 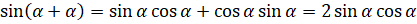 . Получили, что
. Получили, что 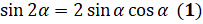 .
.
Тогда формулу косинуса двойного угла можно вывести с помощью формулы сложения для косинуса? Да. В формулу 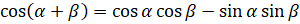 подставим
подставим 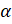 вместо
вместо 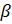 :
: 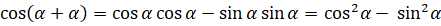 . Таким образом, получили, что
. Таким образом, получили, что 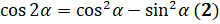 .
.
Давайте вычислим 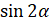 , если
, если 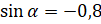 и
и 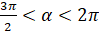 . Воспользуемся формулой
. Воспользуемся формулой 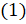 . Значение
. Значение 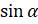 нам известно, а вот значение
нам известно, а вот значение 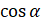 надо найти. Выразим
надо найти. Выразим 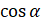 из основного тригонометрического тождества:
из основного тригонометрического тождества: 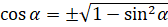 . Так как
. Так как 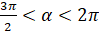 , то есть угол альфа – это угол четвёртой четверти, то
, то есть угол альфа – это угол четвёртой четверти, то 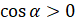 . А значит, можем записать, что
. А значит, можем записать, что 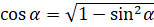 . Подставим значение
. Подставим значение 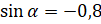 и выполним вычисления:
и выполним вычисления: 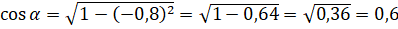 . Теперь подставим значения
. Теперь подставим значения 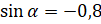 и
и 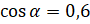 в формулу
в формулу 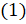 и выполним вычисления:
и выполним вычисления: 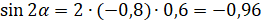 .
.
И давайте вычислим 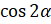 , если
, если 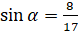 . Воспользуемся формулой
. Воспользуемся формулой 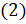 . Значение
. Значение 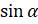 нам известно из условия. Из основного тригонометрического тождества выразим
нам известно из условия. Из основного тригонометрического тождества выразим 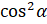 :
: 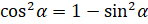 . И подставим в формулу
. И подставим в формулу 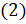 , выполним преобразования:
, выполним преобразования: 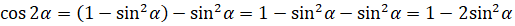 . Затем подставим значение
. Затем подставим значение 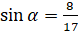 и выполним вычисления:
и выполним вычисления: 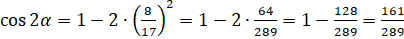 .
.
А сейчас выведем формулу тангенса двойного угла. Для этого в формулу 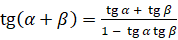 подставим
подставим 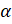 вместо
вместо 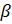 :
: 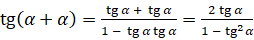 . Получим, что
. Получим, что 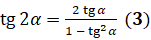 .
.
А есть формула двойного угла для котангенса? Такая формула есть. Но прежде, чем её вывести, давайте докажем следующее равенство: 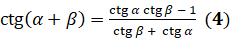 . Перепишем левую часть равенства:
. Перепишем левую часть равенства: 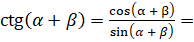 [числитель преобразуем по формуле
[числитель преобразуем по формуле 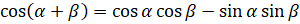 , а знаменатель преобразуем по формуле
, а знаменатель преобразуем по формуле 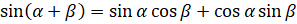 ]
] 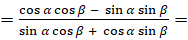 [теперь разделим числитель и знаменатель дроби на
[теперь разделим числитель и знаменатель дроби на 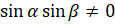 ]
] 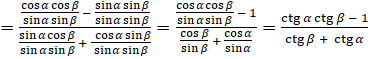 . Равенство
. Равенство 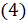 доказано.
доказано.
Это формула сложения для котангенса? Верно. Теперь с помощью этой формулу мы можем вывести формулу котангенса двойного угла. Подставим в формулу 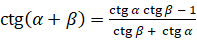 подставим
подставим 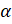 вместо
вместо 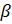 и выполним преобразования:
и выполним преобразования: 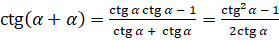 . Таким образом, получили, что
. Таким образом, получили, что 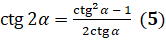 .
.
Давайте вычислим 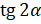 , если
, если 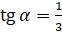 . Подставим в формулу
. Подставим в формулу 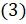 известное значение
известное значение 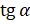 и выполним вычисления:
и выполним вычисления: 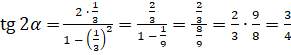 .
.
Таким образом, мы с вами познакомились с формулами синуса, косинуса, тангенса и котангенса двойного угла.
А сейчас закрепим наши знания на практике.
Задание первое. Вычислите: а) 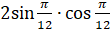 ; б)
; б) 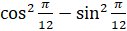 ; в)
; в) 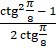 .
.
Решение.
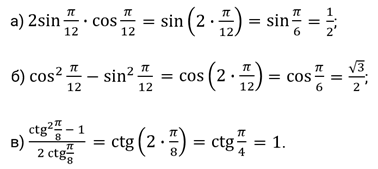
Второе задание. Найдите значение выражений: а) 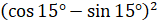 ; б)
; б) 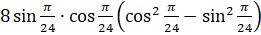 .
.
Решение.
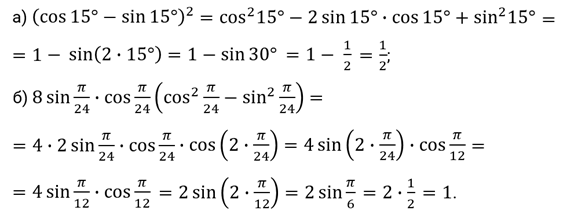
И ещё одно задание. Упростите выражения: а) 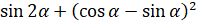 ; б)
; б) 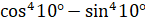 ; в)
; в) 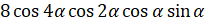 .
.
Решение.