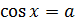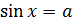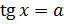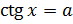Итак, уравнение, которое содержит переменную под знаком тригонометрических функций, называется тригонометрическим уравнением. Уравнения вида , ,  и , где 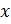 – переменная, а число 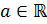, называются простейшими тригонометрическими уравнениями. На этом уроке мы с вами подробно рассмотрим решение уравнений вида .

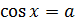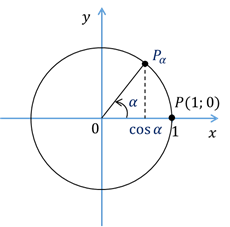
Напомним, что косинусом угла 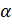 называется абсцисса точки 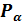, полученной поворотом точки  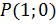вокруг начала координат на угол 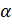. При этом не забудем отметить, что так как координаты  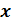и 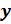 точек единичной окружности удовлетворяют неравенствам  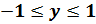и 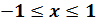, то для  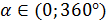справедливо неравенство 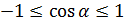. Из этого следует, что уравнение  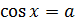имеет корни только при .

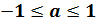Так как же решают такие уравнения? Давайте рассмотрим два уравнения: 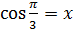 и 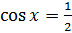. Чтобы найти х в первом уравнении, нам нужно ответить на вопрос, чему равен косинус точки . Для этого нам достаточно вспомнить таблицу значений косинуса.

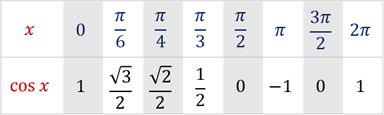
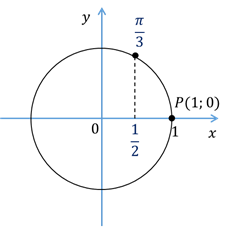
Тогда 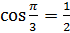. Давайте покажем это на единичной окружности. Отметим точку . У этой точки, как и у любой другой, есть свои координаты. Если мы опустим перпендикуляр из точки  на ось абсцисс, то попадём в .

А теперь вернёмся ко второму уравнению – 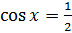. Чтобы здесь найти х, нам нужно ответить на вопрос, косинус каких точек равен .

Давайте ненадолго отвлечёмся от тригонометрии. Начертим координатную плоскость. А теперь найдём все те точки, у которых абсцисса равна . Несложно догадаться, что таких точек будет бесконечное множество и все они будут лежать на вертикальной прямой, проходящей через точки с абсциссой, равной .

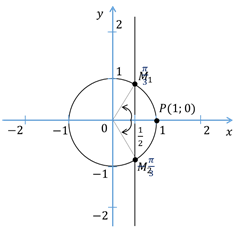
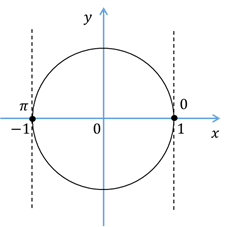
А теперь вернёмся к тригонометрии. Нас будут интересовать все точки, которые лежат на единичной окружности и пересекаются вертикальной прямой, проходящей через точки, имеющие абсциссу, равную . Заметим, что наша прямая пересекает единичную окружность в двух точках – 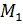 и 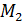. Исходя из таблицы значений косинусов, точка  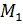получается из начальной точки  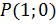поворотом на угол , а тогда точка 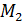 – поворотом на угол 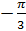. Тогда решением нашего уравнения будут два корня –  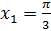и 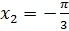. Но ведь в эти точки мы можем попасть не по одному разу. Если мы сделаем полный оборот по единичной окружности, то снова попадём в эти точки. Сделав ещё полный оборот, снова попадём в эти точки и так далее. Отсюда уравнение  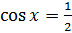имеет две серии решений:

.

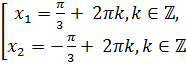Как правило, эти серии решений совмещают и записывают как .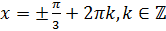

Вообще при решении уравнений вида 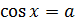 возможны четыре случая.

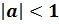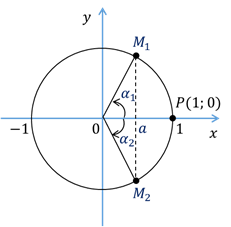
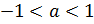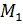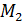Первый случай: . Раскрывая модуль, имеем . В этом случае на единичной окружности будут располагаться две точки –  и , абсциссы которых равны а. Эти точки получаются путём поворота начальной точки на угол  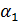и 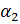 соответственно. Тогда решения уравнения  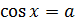можно записать в виде: 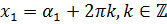, и 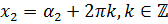. Заметим, что эти точки симметричны относительно оси абсцисс. Следовательно, 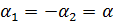. Тогда все решения уравнения  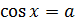можно объединить в одно: .

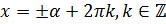Например, решим следующие уравнения 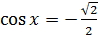 и 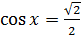. Абсциссу, равную 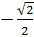, имеют две точки единичной окружности. Так как 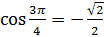, то угол 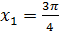, а потому угол 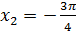. Следовательно, все корни уравнения  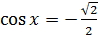можно найти по формуле .

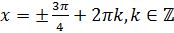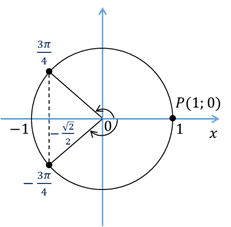
Перейдём к уравнению 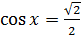. Абсциссу, равную 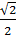, имеют две точки единичной окружности. Так как 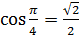, то угол 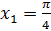, а потому угол 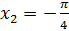. Следовательно, все корни уравнения  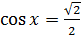можно найти по формуле .

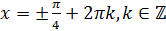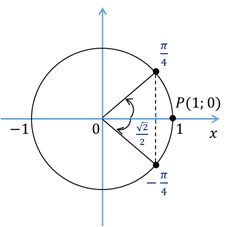
Заметим, что каждое из уравнений 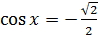 и к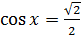 имеет бесконечное множество корней. Однако на отрезке  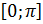каждое из этих уравнений имеет только один корень. Так, 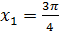, – это корень уравнения 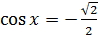, а 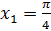, – это корень уравнения 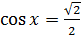. Число  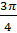называют арккосинусом числа 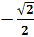. Записывают так: 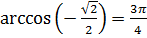. Число  называют арккосинусом числа 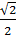. Записывают так: .

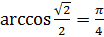Кстати, «арккосинус» в переводе с латинского означает «дуга» и «косинус». Это обратная функция.

Вообще уравнени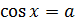е , где 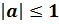, на отрезке  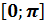имеет только один корень. Если 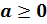, то этот корень заключён в промежутке ;

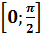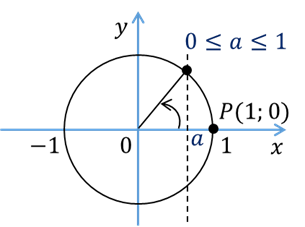
если же 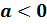, то корень располагается в промежутке .

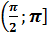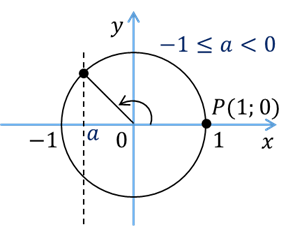
Этот корень называют арккосинусом числа а и обозначают так .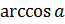

Запомните! Арккосинусом числа а, 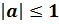, называется такое число 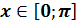, косинус которого равен а.

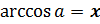, есл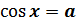и  и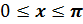 

Например, 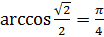, так как 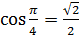, 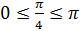. 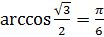, так как , .

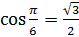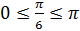Возвращаясь к нашему уравнению 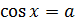, где 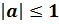, можно утверждать, что все корни уравнения можно найти по формуле: .

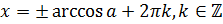Запомните! Для любого 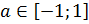 справедлива формула 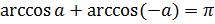. Эта формула позволяет находить значения арккосинусов отрицательных чисел через значения арккосинусов положительных чисел.

Например, .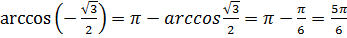

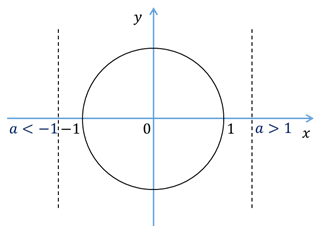
Второй случай: 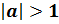. Раскрывая модуль, имеем  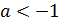и 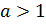. Поскольку для  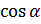справедливо неравенство 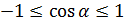, то понятно, что в этом случае уравнение  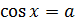не будет иметь корней.

Например, уравнения 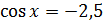 и 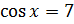 не имеют корней.

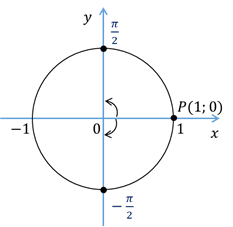
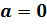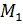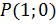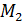Третий случай (частный): . В этом случае есть две точки тригонометрической окружности, которые имеют абсциссу, равную 0. Точка  получается из начальной точки  поворотом на угол , а точка  – поворотом на угол 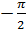. Тогда уравнение  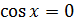имеет две серии решений:

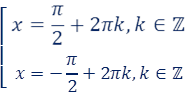
Однако эти две серии решений можно выразить одной формулой: 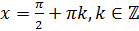. Полученная формула задаёт множество корней уравнения .

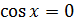И последний, четвёртый случай (тоже частный): 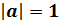. Раскрывая модуль, имеем 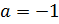, и 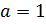. В этом случае вертикальные прямые, проходящие через точки, имеющие абсциссы, равные –1 и 1, будут касаться единичной окружности в точках с координатами (–1;0) и (1;0). Эти точки получаются путём поворота начальной точки на угол 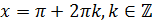, и 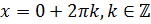. Тогда решением уравнения  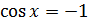будет 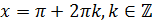, а решением уравнения  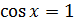будет .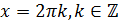

А теперь давайте приступим к практической части нашего урока.

Задание первое. Решите уравнение .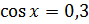

Решение. По формуле нахождения корней уравнения 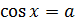, имеем: 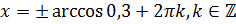. Значение  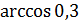вычислим с помощью калькулятора. .

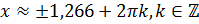Задание второе. Решите уравнение .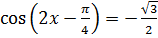

Решение. По формуле нахождения корней уравнения 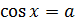, имеем: 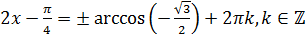. . 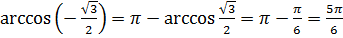Перенесём  в правую часть равенства. Затем разделим обе части равенства на 2: 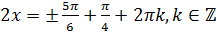. Отсюда .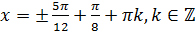