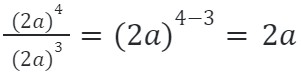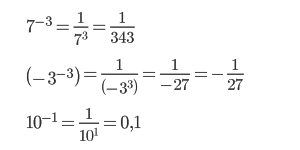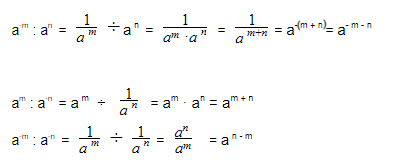Урок№15. Свойства степени с натуральным показателем. (2 часть)

Сложение и вычитание степеней

Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.

2³+ 3⁴= 8 + 81= 89

6³– 3³= 216 – 27 = 189

Сложение степеней с разными показателями

В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.

• 2³+ 2⁴= 8 + 16= 24

Сложение степеней с разными основаниями

В целом это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые показатели. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.

• 3⁴+ 5⁴=81 + 625 = 706
• 1⁴+ 7²= 1+ 49 = 50

Как складывать числа с одинаковыми степенями

Точно так же, как и в предыдущем примере. Если показатели степени одинаковые, а основания разные — нельзя сложить основания и затем эту сумму возводить в степень.

• 6³+ 3³= 216 + 27 = 243

В уравнениях с этим все проще. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a2.

• 2a² + 3a² = 5a²

2,3, 5 — коэффициенты

a²  — переменная

Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.

Вычитание степеней с одинаковым основанием

Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.

• 6³– 3³= 216 – 27 = 189

Вычитание степеней с разными основаниями

Могут быть разные основания, но одинаковые показатели степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.

• 5⁴– 4⁴= 625 – 256 = 369
• 7⁴– 3²= 2401 – 9 = 2392

Вычитание степеней с одинаковыми показателями

Все точно так же, как и со сложением. Если показатели степени одинаковые, а основания разные — нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.

• 6³– 3³= 216 – 27 = 189

И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a²) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a².

• 5a² – 3a² = 2a²

5, 3, 2 — коэффициенты

a²  — переменная

Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.

Умножение и деление степеней

Здесь всё не так однозначно, как со сложением и вычитанием — общие правила для всех случаев выделить не получится. Все зависит от оснований и показателей степеней, с которыми нужно выполнить манипуляции.

Например, действия со степенями с разными основаниями будут отличаться от действий с числами, у которых основания одинаковые. Работа с показателями — одинаковыми и разными — тоже отличается. Давайте разбираться.

Умножение степеней с одинаковыми показателями

Чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:

• aⁿ · bⁿ = (a · b)ⁿ , где

a, b — основание степени (не равное нулю)

n — показатели степени, натуральное число

• a⁵ · b⁵ = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)⁵
• 3⁵ · 4⁵ = (3·4)⁵ = 12⁵ = 248 832
• 16a² = 4²·a² = (4a)²

Умножение степеней с одинаковыми основаниями

Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:

a^m · aⁿ= a^m+n, где

a — основание степени

m, n — показатели степени, любые натуральные числа

• 3⁵ · 3² = 3^{5 + 2} = 3⁷ = 2 187
• 2⁸ · 8¹= 2⁸ · 2³ = 2^{8 + 3} = 2¹¹ = 2048

Умножение степеней с разными основаниями и показателями

Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 2⁸ · 8¹= 2⁸ · 2³ = 2¹¹ = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:

• 3³ · 5² = 27·25 = 675

Деление степеней с одинаковыми основаниями и одинаковыми показателями

Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

• 
• 

Деление чисел с одинаковыми показателями степени

При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:

• aⁿ : bⁿ = (a : b)ⁿ , где

a, b — основание степени, любые числа, b ≠ 0,

n — показатель степени, натуральное число

Пример:

Деление степеней с разными основаниями и показателями

Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:

• 3³ ÷5² = 27÷25 = 1,08

Степень с отрицательным показателем и её свойства

Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:

Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.

Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.

Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:

• a³÷a⁶=a^{3 – 6} = a^-3

Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:

Умножение отрицательных степеней

При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:

a^m · aⁿ = a^m+n

Деление отрицательных степеней

При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:

Возведение дроби в отрицательную степень

Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:

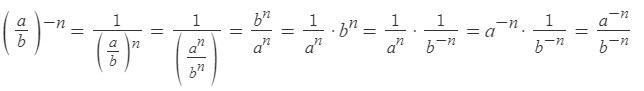
Возведение произведения в отрицательную степень

Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:

Как представить число в виде степени

Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.

Например, представим в виде степени число 243:

243 = 3 × 3 × 3 × 3 × 3 = 3⁵