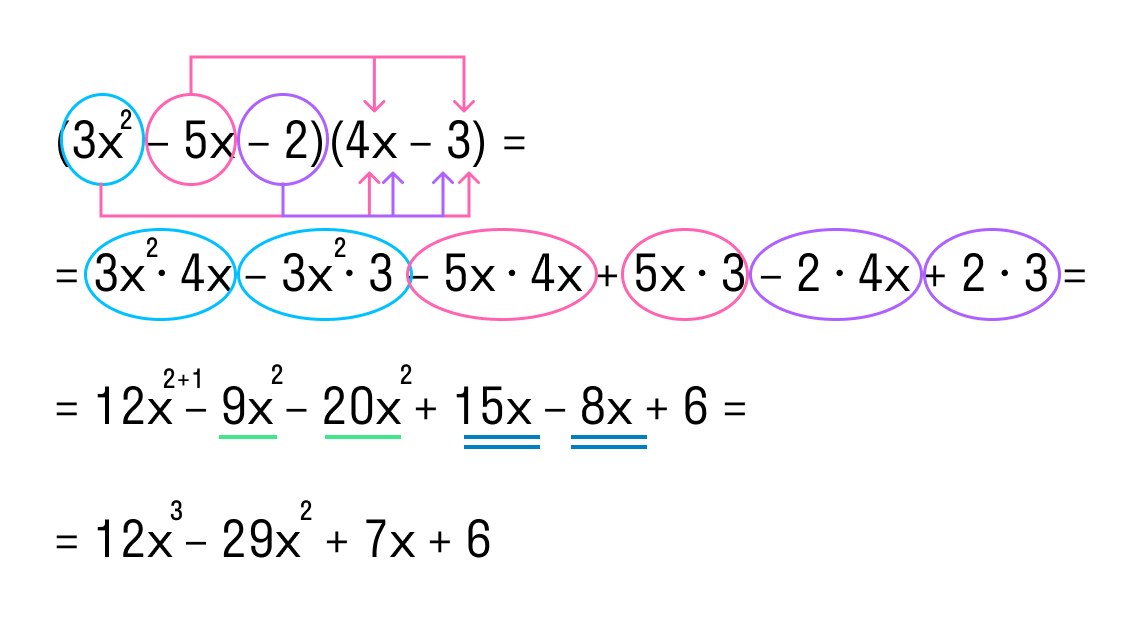Алгебра 7 класс. Урок№22. Умножение многочлена на многочлен.

Правило умножения многочлена на многочлен

Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:

• Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
• Сначала составим их произведение: (a + b)(c + d).
• Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
• Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
• Проведем обратную замену x на (c + d):
  a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd.
• Как изменилось произведение исходных многочленов:
  (a + b)(c + d) = ac + ad + bc + bd.
  Как раз так и выглядит формула умножения многочлена на многочлен.

Алгоритм умножения многочлена на многочлен:

1. • Первый член первого многочлена умножить на каждый член второго многочлена. Второй член первого многочлена умножить на каждый член второго многочлена. И так далее.

• • Сложить полученные произведения.

• • Преобразовать полученную сумму в многочлен стандартного вида.

Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).

Как решаем:

• Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
• Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.

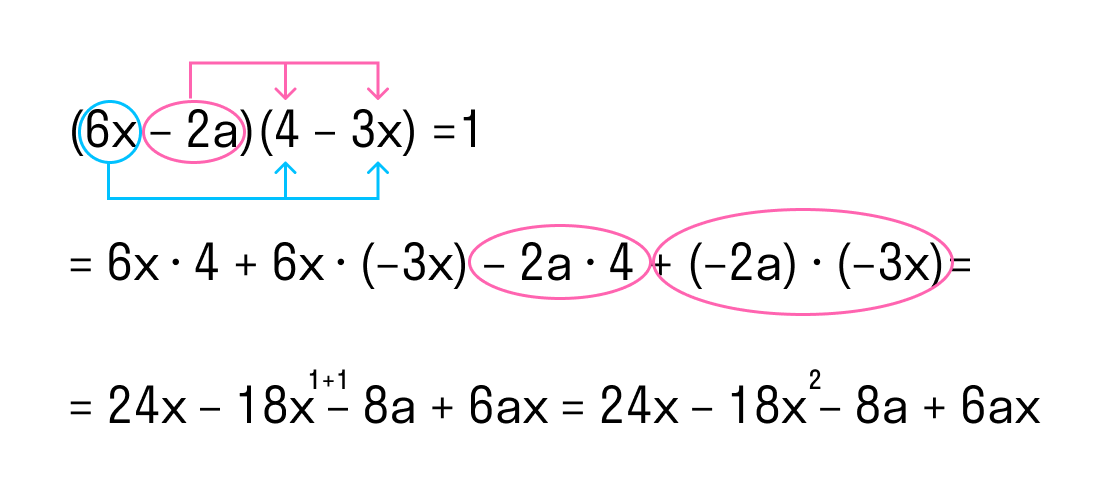
Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x² – 8a + 6ax.

Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).

Как решаем:

• Умножим первый многочлен на второй. Результат запишем в скобках.
  
• Перемножим получившийся многочлен и третий многочлен. Приведем подобные одночлены.
  

Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x³ – 29x² + 7x + 6.

Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.

Примеры умножения многочлена на многочлен

Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.

Пример 1. Выполнить умножение многочленов:
2 − 3x и x² − 7x + 1.

Как решаем:

Запишем произведение: (2 − 3x)(x² − 7x + 1).

Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x² − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x², 2(−7x) и 2*1.

Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx², −3x(−7x) и −3x*1.

Из полученных выражений составим сумму: 2x² + 2(−7x) + 2*1 − 3xx² − 3x(−7x) − 3x*1.

Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.

Осталось полученную сумму преобразовать в многочлен стандартного вида:

2x² + 2(−7x) + 2*1 − 3xx² − 3x(−7x) − 3x*1 = 2x² − 14 x + 2 − 3x³ + 21x² − 3x = (2x² + 21x²) + (−14x − 3x) + 2 − 3x³ = 23x² − 17x + 2 − 3x³.

Получается, что (2 − 3x)(x² − 7x + 1) = 23x² − 17x + 2 − 3x³.

Ответ: (2 − 3x)(x² − 7x + 1) = 23x² − 17x + 2 − 3x³.

Пример 2. Найти произведение трех многочленов:
x² + xy − 1, x + y и 2y − 3.

Как решаем:

Запишем их произведение: (x² + xy − 1)(x + y)(2y − 3).

Умножим первые два многочлена:

(x² + xy − 1)(x + y) = x²x + x²y + xyx + xyy − 1x − 1y = x³ + 2x²y + xy² − x − y.

Таким образом: (x²+ xy − 1)(x + y)(2y − 3) = (x³ + 2x²y + xy² − x − y)(2y − 3).

Снова выполним умножение двух многочленов:

(x³ + 2x²y + xy² − x − y)(2y − 3) = x³2y + x³(−3) + 2x²y²y + 2x²y(−3) + xy²2y + xy²(−3) − x²y − x(−3) − y²y − y(−3) = 2x³y − 3x³ + 4x²y² − 6x²y + 2xy³ − 3xy² − 2xy + 3x − 2y² + 3y.

Ответ: (x² + xy − 1)(x + y)(2y − 3) = 2x³y − 3x³ + 4x²y² − 6x²y + 2xy³ − 3xy² − 2xy + 3x − 2y² + 3y.