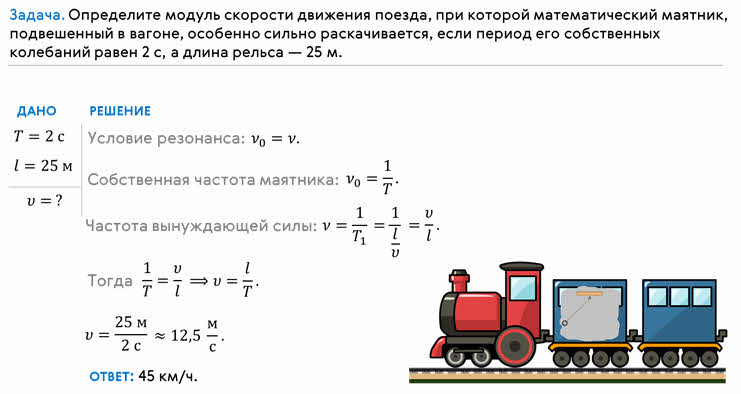
На прошлых уроках мы с вами знакомились с колебательным движением и простейшими колебательными системами — математическим и пружинным маятниками. При этом мы считали, что их колебания являются свободными (то есть происходят только под действием внутренних сил), и подчиняются гармоническому закону.
Напомним, что системы, на которые не действуют внешние силы, — это замкнутые системы. А, мы уже знаем, что в замкнутой системе полная механическая энергия остаётся постоянной и равной той энергии, которую мы изначально ей сообщили. Поэтому свободные колебания — это колебания с постоянной амплитудой. А маятник, выведенный из положения равновесия, должен колебаться вечно!
Иногда действительно можно наблюдать колебания, длящиеся достаточно долго. Например, если очень длинный маятник отклонить на небольшой угол, то он сможет в течение многих часов совершать колебания с постоянной амплитудой. Однако, как бы долго ни продолжались свободные колебания, маятник в конце концов все-таки останавливается. Говорят, что колебания затухают. «Виновата» в этом сила трения, которая в реальных земных условиях действует на всё, что движется.
Колебания с уменьшающейся амплитудой называются затухающими колебаниями. Причём чем больше силы сопротивления движению, тем быстрее прекращаются колебания. Например, в воде колебания затухают гораздо быстрее, чем в воздухе.
Конечно же затухающие колебания нельзя считать свободными, поскольку свободные колебания — это колебания, происходящие с постоянной амплитудой.
— Каким же образом можно добиться того, чтобы колебания не затухали?
Очевидно, что необходимо восполнять потери энергии за каждый период колебаний. Для этого нужно воздействовать на колеблющееся тело периодически изменяющейся силой. Например, если каждый раз подталкивать маятник в такт его колебаниям, то он сможет качаться сколь угодно долго.
Такие колебания, то есть колебания, происходящие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями.
А периодическая сила, вызывающая такие колебания, называется вынуждающей силой.
Таким образом, колебательная система, на которую действует внешняя периодическая сила, совершает вынужденные колебания, частота которых равна частоте вынуждающей силы. При этом амплитуда вынужденных колебаний при данной частоте вынуждающей силы не изменяется, даже если на систему будут действовать силы сопротивления, так как потери энергии компенсируются работой вынуждающей силы.
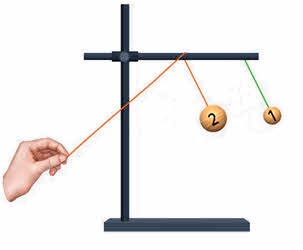
Давайте выясним, зависит ли амплитуда вынужденных колебаний от соотношения между частотой вынуждающей силы и собственной частотой колебательной системы. Для этого проведём такой опыт. Подвесим на нитях, прикреплённых к общей перекладине два маятника — маятник один и маятник два, имеющий массу существенно больше.
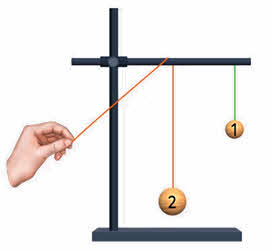
Длина нити первого маятника постоянна, а длину второго можно изменять, подтягивая свободный конец нити, при этом будет изменяться и его собственная частота колебаний. Если привести в движение маятник большей массы, то он через перекладину будет действовать на маятник один с некоторой вынуждающей силой, изменяющейся с такой же частотой, с какой колеблется маятник два.
Если мы будем уменьшать длину второго маятника частота его колебаний увеличится. При этом увеличится и частота вынуждающей силы, действующей на первый маятник, при этом начнёт увеличиваться и его амплитуда. Увеличение амплитуды будет продолжаться до тех пор, пока длины маятников не станут равными.
Когда длины маятников становятся равными, то есть когда частота вынуждающей силы совпадает с частотой собственных колебаний первого маятника, его амплитуда колебаний резко возрастает. При дальнейшем уменьшении длины маятника два частота вынуждающей силы оказывается больше собственной частоты маятника один и амплитуда его колебаний уменьшается.
Явление резкого возрастания амплитуды вынужденных колебаний при равенстве частот вынуждающей силы и собственной частоты колебательной системы называется резонансом.
Явление резонанса можно продемонстрировать и на таком опыте. Подвесим на рейку несколько маятников разной длины.
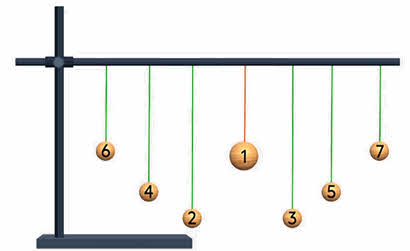
Пусть центральный маятник будет массивным, а остальные — лёгкими. Приведём центральный маятник в движение в плоскости, перпендикулярной рейке. Он будет совершать свободные колебания, периодически действуя с некоторой силой на рейку. Рейка будет передавать это воздействие остальным маятникам, которые начнут совершать вынужденные колебания с частотой колебаний массивного маятника.
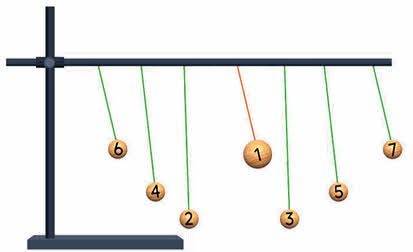
Обратите внимание, что маятники 2 и 3 останутся почти неподвижными, так как их собственные частоты значительно отличаются от частоты массивного маятника. Амплитуды маятников 4 и 5 будут больше, а маятники 6 и 7, имеющие ту же длину нити, что и массивный маятник, начнут колебаться с очень большой амплитудой, то есть войдут в резонанс с массивным маятником.
В чем причина явления резонанса? Почему растёт амплитуда колебаний, когда частота вынуждающей силы приближается к частоте собственной?
Дело в том, что совпадение частот означает, что равнодействующая силы тяжести и силы упругости нити в самой системе действует «в такт» с вынуждающей силой. Если равнодействующая и вынуждающая силы в какие-то моменты действуют в одном направлении, то они складываются и их действие усиливается. И даже если вынуждающая сила мала, она всё равно приведёт к росту амплитуды, так как она добавляется к равнодействующей силе каждый период.
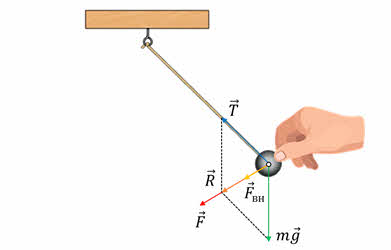
Явление резонанса может быть полезным, поскольку оно позволяет получить даже с помощью малой силы большое увеличение амплитуды колебаний. Например, тяжёлый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.
С другой стороны, резонансные явления могут вызвать необратимые разрушения в различных механических системах. Известны случаи, когда вследствие резонанса в воздухе рассыпался на части самолёт, ломались гребные винты у кораблей, разрушалась железная дорога.
Что бы не допустить резонанса, изменяют собственную частоту системы или частоту вынуждающей силы. Для этого, например, поезда переезжают мосты или очень медленно, или с максимальной скоростью, что бы частота ударов колёс о стыки была либо меньше, либо больше собственной частоты колебаний моста. А солдаты, переходя через мост, идут не в ногу, а сбивают шаг. Иначе, если частота их шагов совпадёт с частотой собственных колебаний моста, он может разрушится. Так произошло в 1850 году вблизи города Анже во Франции, когда через мост Бас-Шен, висящий на цепях, проходил отряд солдат. В результате обрушения погибло 226 человек.
Похожий случай произошёл и в Петербурге в январе 1905 года, при переходе кавалерийского эскадрона по Египетскому мосту через реку Фонтанка. По счастливой случайности, никто из людей не погиб.
А 7 ноября 1940 года сильный порыв ветра вызвал резонансные колебания Такомского моста в США, что привело к его разрушению.
В тех случаях, когда резонанс может нанести ущерб, принимают меры к тому, чтобы не допустить его возникновения. Например, многие заводские станки, отдельные части которых совершают периодические движения, устанавливают на массивном фундаменте или амортизаторных пружинах, препятствующих возникновению колебаний всего станка.
На явлении резонанса основано действие частотомера, с помощью которого измеряют частоту колебаний.

Закрепления материала.