Момент силы
«Кто овладел творениями Архимеда,
будет меньше удивляться открытиям
самых великих людей нашего времени»
Г.В. Лейбниц
В данной теме разговор пойдёт о моменте силы.
В прошлой теме говорилось о простых механизмах, которые служат для преобразования механического действия на тело, позволяя изменить точку приложения силы, ее модуль и направление. Выяснили, что рычагом является любое твердое тело, которое может поворачиваться относительно неподвижной опоры или оси.
Разделили рычаги на два вида — рычаг первого и рычаг второго рода. Рычагом первого рода называется рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону. Рычагом второго рода называется рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу. Расстояние от точки опоры до прямой, вдоль которой действует сила, называется плечом силы.
Вывели условие равновесия рычага, согласно которому, рычаг находится в равновесии при условии, что приложенные к нему силы обратно пропорциональны длинам их плеч.
Применим основное свойство пропорции для условия равновесия рычага. Тогда условие равновесия рычага примет вид:
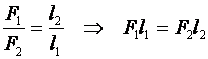
Произведение модуля силы на ее плечо — это новая физическая величина, которая называется моментом силы (обозначается буквой М).
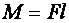
Измеряется момент силы в Ньютон-метрах (Н·м).
[M] = [Н·м]
Момент силы характеризует действие силы и показывает, что это действие зависит как от модуля силы, так и от ее плеча.
Сформулируем условие равновесия рычага через правило моментов: рычаг под действием двух создающих моменты сил находится в равновесии в том случае, если момент силы, вращающей рычаг по часовой стрелке, равен моменту силы, вращающей рычаг против часовой стрелки.
В рассмотренном в прошлой теме опыте силы, действующие на рычаг, были равны, соответственно, 8 Н и 4 Н, а их плечи составляли 2,5 и 5 делений рычага соответственно. Т.е. моменты этих сил равны при равновесии рычага.
А возможно ли равновесие рычага, когда на него действует более двух сил? Да, возможно. Рассмотрим рисунок.
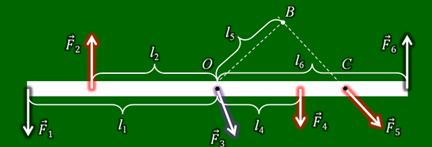
На нем изображен рычаг и несколько сил, действующих на него. Чтобы такой рычаг находился в равновесии нам необходимо:
1. Найти сумму моментов всех сил, вращающих рычаг по часовой стрелке.
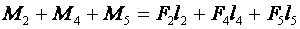
Необходимо отметить, плечо силы F5 — это не расстояние OC, а расстояние OB — кратчайшее по перпендикуляру к прямой CB.
2. Найти сумму моментов сил, вращающих рычаг против часовой стрелки.
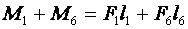
3. Сравнить сумму моментов всех сил, вращающих рычаг по часовой стрелки и сумму моментов сил, вращающих рычаг против часовой стрелки.
И если эти суммы равны между собой, то рычаг будет находиться в равновесии.
Возникает вопрос: Почему не учли силу F3? Если посмотреть на рисунок, то можно заметить, что плечо этой силы равно нулю. Значит и момент ее равен нулю, и она не влияет на равновесие рычага.
Правило моментов (или условие равновесия рычага) лежит в основе действия различного вида инструментов и устройств, применяемых как в технике, так и в быту там, где требуется получить выигрыш в силе.
Давайте рассмотрим некоторые из них.
Ножницы — рычаг первого рода, ось вращения которого проходит через винт, соединяющий их две половинки. В зависимости от назначения, устройство ножниц бывает различным.

Например, для резки бумаги применяются ножницы, длина лезвий которых сопоставима с длиной ручек, так как при резке бумаги нет необходимости прикладывать большую силу. Ножницы, предназначенные для резки металла, имеют более длинные, по сравнению с размерами лезвия, ручки, так как сила сопротивления металла достаточно большая. И для того чтобы ее уравновесить, необходимо увеличивать плечо действующей силы. А в кусачках — инструменте, предназначенном для «перекусывания» проволоки — разница между длиной режущей части и ручками еще больше.
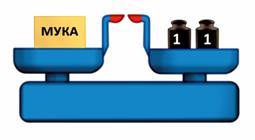
Рычаги можно обнаружить и в педалях автомобиля, и в клавишах пианино, рукоятки тисков и рычаге сверлильного станка. Также на принципе рычага основано действие рычажных весов. Например, учебные весы или весы, стоящие в магазинах, действуют как равноплечий рычаг.
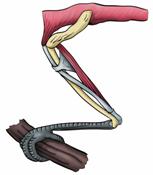
Множество рычагов можно найти в теле человека, животных, насекомых и птиц. Две кости, соединенные суставом и мышца, прикрепленная к этим костям, и представляют собой самый обычный рычаг.
Рычаги присутствуют даже в растениях. Для примера рассмотрим шалфей обыкновенный. Хоть он и называется «обыкновенным», но он не такой простой цветок.

По своей форме его цветки немного напоминают раскрытую пасть змеи. Из-под верхней «губы» даже высовывается «жало» — это две далеко вытянутые тычинки цветка. Внутри цветка на дне крохотной воронки светится капелька сладкого нектара. Этим нектаром шалфей приманивает шмеля, который и опыляет его. Как только насекомое залезает внутрь цветка за нектаром, из-под верхнего лепестка появляются две тычинки на длинных ножках и касаются спинки шмеля, обсыпая ее пыльцой. Потом шмель перелетает на другой цветок шалфея, залезает внутрь, и пыльца с его спинки попадает прямо на рыльце пестика, а цветку только это и нужно.
Где же у цветков шалфея рычаг? Оказывается, это тычинки с пыльцой. От оси у тычинок цветка отходят два плеча— длинное и короткое. На конце длинного, похожего на коромысло, плеча висит пыльцевой мешочек. А короткое плечо сплющено и закрывает вход в глубину цветка. Подтянется шмель своим хоботком к нектару и обязательно толкнет короткое плечо. А оно тотчас приведет в движение длинное плечо-коромысло. То в свою очередь ударяет по спине шмеля своими пыльниками — вот и сработал рычаг. А шмель летит дальше, касается рыльца пестика нового цветка и опыляет его.



Упражнения.
Задача 1. Определите, с какой силой натянута мышца бицепса при подъеме ядра массой 10 кг, если расстояние от центра ядра до локтя составляет 32 см, а от локтя до места крепления мышцы — 4 см?

Задача 2. На рисунке изображен рычаг, на котором имеются крючки, прикрепленные через одинаковые расстояния. Крючки пронумерованы от минус 3 до 3, причем ноль приходится на середину рычага. К некоторым крючкам прикреплено по нескольку грузов одинаковой массы. Имеется еще один такой же не подвешенный груз. К крючку с каким номером его нужно подвесить, чтобы рычаг находился в равновесии?

Основные выводы:
– Момент силы — это физическая величина, равная произведению модуля силы, вращающей тело, на ее плечо.
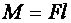
– Единицей измерения момента силы является Ньютон-метр.
[M] = [Н·м]
– Правило моментов: рычаг под действием двух создающих моменты сил находится в равновесии в том случае, если момент силы, вращающей рычаг по часовой стрелке, равен моменту силы, вращающей рычаг против часовой стрелки.