На прошлом уроке мы с вами рассматривали неравномерное движение и самый простой его вид — прямолинейное равноускоренное движение. Давайте вспомним, что это такое движение, при котором тело движется вдоль прямой, а проекция его вектора скорости за любые равные промежутки времени изменяется одинаково.
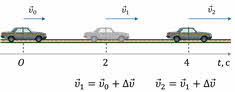
Для характеристики такого движения вводится понятие мгновенной скорости, то есть скорости в данный момент времени или в данной точке траектории.
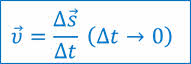
А также величина, называемая ускорением. Ускорение — это физическая векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
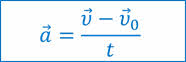
Из формулы для ускорения, выполнив небольшие преобразования, легко получить формулу для определения скорости тела в любой момент времени:
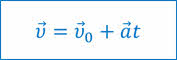
Полученное уравнение называется уравнением скорости.
При вычислении скорости, как и в случае с ускорением, мы будем пользоваться формулой, в которую входят не векторы, а их проекции на координатную ось:
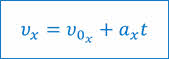
Вы уже знаете, что описать механическое движение тела можно не только с помощью формул, но и с помощью графиков. Давайте рассмотрим, как строятся такие графики на примере равноускоренного движения шарика по наклонному жёлобу. Пусть в начальный момент времени скорость шарика была равна v0, а в конце жёлоба — v. Ускорение шарика мы обозначим через a.
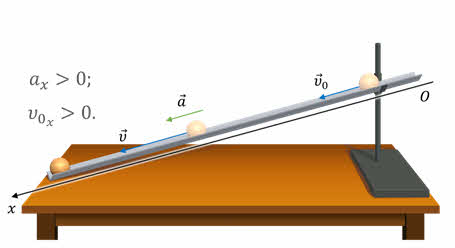
Направим координатную ось Ox вдоль жёлоба по направлению движения шарика. Тогда проекция векторов начальной скорости и ускорения на выбранную координатную ось будут положительными.
Построим график зависимости проекции ускорения от времени. Так как модуль ускорения с течением времени не меняется, а проекция ускорения положительна, то графиком будет являться прямая линия, параллельная оси времени, расположенная выше этой оси.

Теперь исследуем график зависимости проекции скорости от времени. Из курса математики вам известна функция, вида
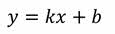
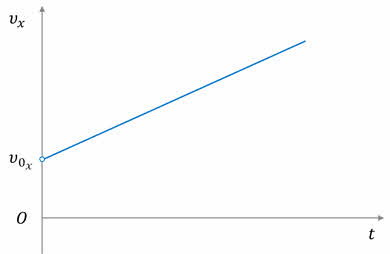
Графиком этой функции является прямая линия. Функция зависимости проекции скорости от времени тоже линейная с аргументом t, постоянным коэффициентом axи свободным членом v0x. Значит, графиком этой функции тоже является прямая линия, расположение которой по отношению к осям координат определяется значениями проекций начальной скорости и ускорения.
Рассмотрим другой пример — движение шарика вверх по наклонному жёлобу.
Теперь начальная скорость шарика направлена вдоль жёлоба вверх. Двигаясь вверх, шарик будет постепенно терять скорость. В некоторой точке он на мгновение остановится и начнёт скатываться вниз. Точку, в которой шарик на мгновение остановился, называют точкой поворота.
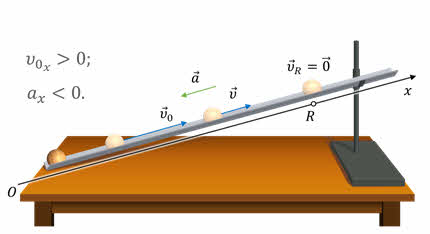
Как и в прошлом примере, направим координатную ось вдоль жёлоба по направлению движения шарика. Тогда, проекция вектора начальной скорости на ось будет положительной, а проекция вектора ускорения — отрицательной.
Следовательно, графиком зависимости проекции ускорения от времени будет являться прямая линия, параллельная оси времени, расположенная ниже этой оси.

А графиком зависимости проекции скорости от времени является прямая линия, расположение которой по отношению к осям координат определяется значениями проекций начальной скорости и ускорения.
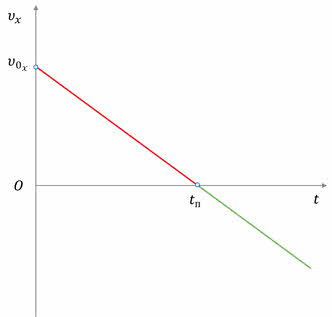
График скорости показывает, что вначале, пока шарик двигался вверх, проекция скорости была положительна. Она уменьшалась и в некоторый момент времени стала равной нулю. В этот момент шарик достиг точки поворота. В данной точке направление скорости шарика изменилось на противоположное — проекция скорости стала отрицательной.
По графику зависимости проекции скорости на ось Ох от времени можно определить проекции ускорения тела на эту ось. Для этого на графике достаточно выбрать два произвольных момента времени и найти изменение скорости за этот промежуток времени. А дальше воспользоваться формулой для определения проекции ускорения при равноускоренном движении.
Закрепления материала.
На рисунке приведены графики зависимости от времени проекций скоростей двух тел. Постройте графики зависимости проекций ускорений от времени для каждого тела.
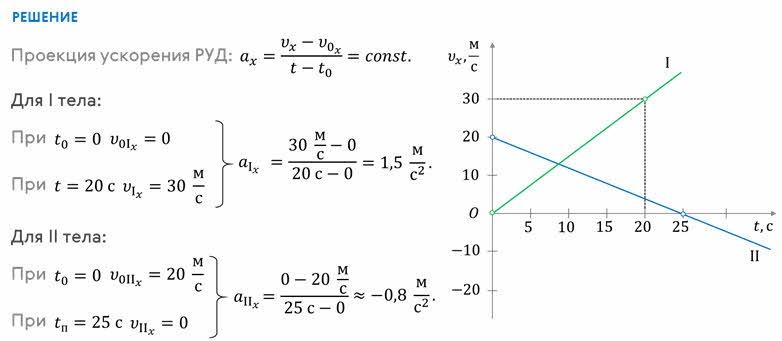
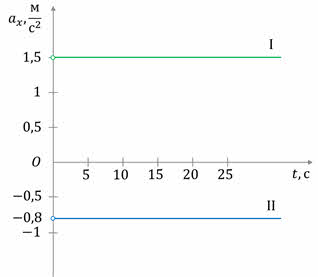
Домашняя работа
Стр. 25 — 28
Упр. 6
Электронный учебник: http://urok55.ru/%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0-9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D1%83%D1%87%D0%B5%D0%B1%D0%BD%D0%B8%D0%BA/