Физические величины. Точность и погрешность измерений
Измерять – значит, познавать
Данная тема посвящена физическим величина и их измерениям. В физике часто приходится измерять те или иные величины. Измерить можно высоту дома или длину улицы.

Можно измерить объём воды в колбе или массу воды в стакане.
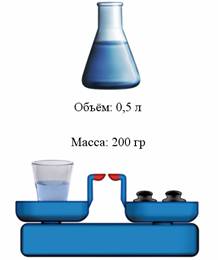
Но что означают эти измерения? Измерить какую-либо величину – значит сравнить её с однородной величиной, принятой за единицу. Из приведённых выше примеров, можно заметить, что, например, единицей объёма является литр, а единицей массы является грамм. Для удобства была введена международная система единиц, которая называется СИ.

В этой системе длина измеряется в метрах, масса в килограммах, объём — в кубических метрах, время – в секундах и так далее. В процессе изучения физики будут вводиться новые величины и соответствующие им единицы измерения. Иногда физические величины можно не измерять, а вычислять по формуле. Например, для того, чтобы вычислить среднюю скорость нужно пройденное расстояние разделить на время. То есть, данная формула помогает вычислить такую физическую величину, как средняя скорость.
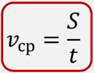
Известно что, иногда применяются единицы измерения, которые в десятки, сотни, тысячи и так далее раз больше принятых единиц измерения. Такие единицы измерения называются кратными.
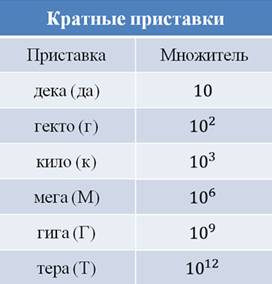
Каждая приставка соответствует тому или иному множителю. Например, «Дека» означает в 10 раз больше, «гекто» — в сто раз больше, «кило» — в тысячу раз больше, «мега» — в миллион раз больше и так далее. Необходимо отметить, что в физике принято записывать такие множители в виде степени числа 10. Например, вместо миллиона записывается 106. Также, могут быть использованы единицы, которые в десятки, сотни, тысячи и так далее раз меньше принятых единиц измерения. Такие единицы измерения называются дольными.
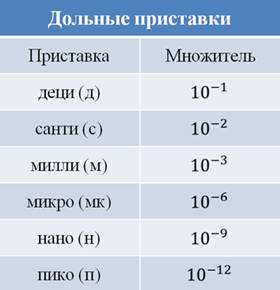
Каждая приставка соответствует тому или иному множителю. Например, «Деци» означает в 10 раз меньше, «санти» — в сто раз меньше, «милли» — в тысячу раз меньше, «микро» — в миллион раз меньше и так далее. Эти приставки также записываются в виде степени числа 10. Например, вместо записи числа 0,000001 записывается 10–6.
У каждого ученика имеется линейка, длина которой измеряется в сантиметрах, то есть в единицах, которые в сто раз меньше метра. Поэтому, если длина линейки составляет 15 сантиметров, мы можем сказать, что её длина 0,15 метра.

Линейка – это прибор для измерения длины. Конечно, линейка относится к самым простым измерительным приборам. Существуют значительно более сложные приборы: например, термометр, который применяется для измерения температуры, гигрометр, который используется для измерения влажности или амперметр, который используется для измерения силы электрического тока.


Важно знать, как пользоваться измерительными приборами и насколько могут быть точны те или иные измерения. У каждого ученика есть линейка и карандаш. Можно попытаться измерить длину карандаша. В первую очередь нужно определить, какова цена деления измерительного прибора. Для этого необходимо найти два ближайших штриха шкалы, возле которых указаны значения величины (например, 1 см и 2 см). Далее нужно сосчитать число делений, заключенных между цифрами 1 и 2. При подсчёте получается, что количество этих делений равно 10. Таким образом, между отметками 1 см и 2 см заключено десять делений. Вычитаем из большего числа меньшее и делим на количество делений между ними. В результате вычислений получаем, что цена деления линейки составляет 0,1 см или 1 мм. Данный пример объясняет, как определить цену деления любого измерительного прибора.
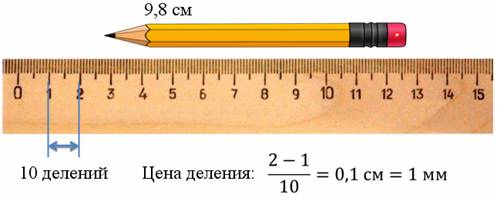
Как видно из рисунка, длина карандаша чуть меньше десяти сантиметров. Если бы на этой линейке не было миллиметровых делений, то можно было сказать, что длина карандаша равна десяти сантиметрам. Но это было бы не совсем точное измерение. Такую неточность называют погрешностью измерения. В представленном случае, на линейке есть миллиметровые деления, поэтому можно измерить длину карандаша с более высокой точностью – 9,8 см. Это говорит о том, что чем меньше цена деления, тем больше точность измерения. Ну а большая точность измерения означает меньшую погрешность. Однако абсолютно точных измерений не существует. Если дать один и тот же карандаш каждому ученику из класса и попросить измерить длину карандаша, не у всех получится одинаковый результат. Тем не менее, погрешность измерения не может быть больше цены деления. Например, если видно, что длина карандаша не точно 9,8 см, а чуточку больше, то понятно, что длина карандаша находится в промежутке от 9,8 см до 9,9 см.
Погрешность измерений принято считать равной половине цены деления измерительного прибора. То есть, в рассмотренном случае, погрешность измерений составляет 0,5 мм. Поэтому, после того, как измерили карандаш и записали, что его длина равна 9,8 см, следует записать погрешность.
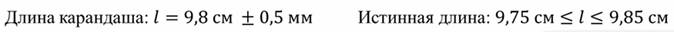
Знак «±» означает, что указанная длина может быть на полмиллиметра больше или на полмиллиметра меньше. Таким образом, истинное значение длины карандаша находится в промежутке от 9,75 см до 9,85 см.
В общем случае запись измеряемых величин с учетом погрешности имеет следующий вид:
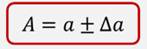
где А – измеряемая величина;
а – результат измерения;
Da – погрешность измерений.
Необходимо отметить, что при сложении или вычитании величин с погрешностью, погрешность результата равна сумме погрешностей каждой величины. В этом легко убедиться на примере. На рисунке показаны два отрезка AB и CD, длины которых измерены с определенной погрешностью.

Рассчитаем сумму длин этих отрезков. Из рисунка видно, что отрезок AB равен 1 м ± 1 см. Истинная длина этого отрезка находится в промежутке 99 см ≤ АВ ≤ 101 см. Отрезок CD равен 12 см ± 0,5 см. Истинная длина этого отрезка находится в промежутке от 11,5 см ≤ CD ≤ 12,5 см. Поэтому, сумма длин этих отрезков будет иметь еще большую погрешность. Прежде чем производить вычисления, необходимо перевести обе длины в одинаковые единицы измерения.
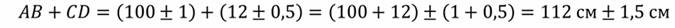
Таким образом, получаем, что сумма длин отрезков AB и CD равна
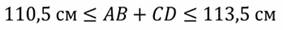
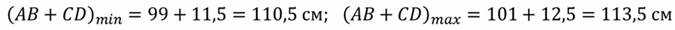
Важно отметить, что этот же промежуток мы бы получили, если бы сложили наименьшие и наибольшие длины отрезков AB и CD. Следовательно, при сложении или вычитании величин, измеренных с погрешностями, погрешность результата равна сумме погрешностей каждой из величин.
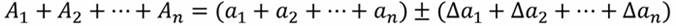
Упражнения.
Упражнение 1. Заполните таблицу, указав, что из перечисленных слов является физическим телом, единицей измерения, физической величиной или физическим явлением: ветер, Луна, килограмм, дерево, длина, скорость, испарение.
Решение:

Упражнение 2. Родители измерили рост братьев Димы и Васи с помощью рулетки, цена деления которой 1 см. Подсчитайте, насколько см Дима выше, чем Вася.
Решение:

Упражнение 3. Найдите суммарную массу животных с погрешностью.
Решение:

Основные выводы:
– Для описания физических тел или физических явлений вводится физическая величина, которую можно измерить с помощью измерительных приборов или вычислить по формуле.
– Измерение величины – это сравнение её с однородной величиной, принятой за единицу.
– Кратные приставки – это приставки означающие увеличение в десятки, сотни, тысячи и так далее раз.
– Дольные приставки – это приставки, означающие уменьшение в десятки, сотни, тысячи и так далее раз.
– Погрешность измерений – неточность допускаемая при измерении. За погрешность измерений данного прибора принимают половину цены деления этого прибора.
– При сложении или вычитании величин с погрешностями, погрешность результата вычислений равна сумме погрешностей каждой величины.
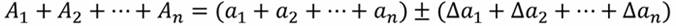
Домашнее задание
Страница 8 — 14 читать
Ответы на вопросы в конце параграфов