Частным случаем проявления силы всемирного тяготения является сила притяжение тел к Земле, также называемая силой тяжести, с которой вы знакомились ещё в седьмом классе.
Напомним, что сила тяжести, действующая на тело, равна произведению массы тела и ускорения свободного падения:
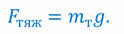
Однако, помимо известной нам формулы, силу тяжести можно рассчитать исходя из закона всемирного тяготения:
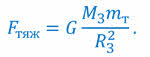
Строго говоря, эти две силы не равны, так как Землю, из-за её вращения вокруг своей оси, нельзя считать инерциальной системой отсчёта. Но эти различия настолько малы, по сравнению с самими силами, что их можно считать приблизительно равными:
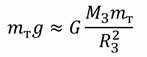
Разделив полученное выражение на массу тела, получим, что ускорение свободного падения прямо пропорционально массе Земли и обратно пропорционально квадрату её радиуса:
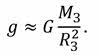
Как видно из формулы, величина ускорения свободного падения не зависит от массы тела и характеризует лишь само гравитационное поле Земли и, как следствие, одинаково для всех тел. Таково необычное свойство силы тяжести, а значит, и вообще силы всемирного тяготения. Необычное оно потому, что по второму закону Ньютона ускорение должно быть обратно пропорционально массе тела. Но закон всемирного тяготения объяснил эту странность: сила всемирного тяготения потому сообщает всем телам одинаковые ускорения, что сама она пропорциональна массе того тела, на которое действует.
Значение ускорения свободного падения зависит от многих факторов. Главные из них — это географическая широта местности, высота над уровнем моря и плотность породы в толще Земли в месте наблюдения.
Рассмотрим каждую зависимость отдельно. Вы знаете, что планета Земля несколько сплюснута у полюсов, и расстояние от центра Земли до её поверхности у полюсов меньше, чем на экваторе. Вместе с тем Земля вращается, и, следовательно, различные точки на её поверхности имеют разные ускорения по отношению к ИСО, связанной с Солнцем. Это приводит к тому, что ускорение свободного падения на разных широтах различно. Но для определённой широты местности ускорение свободного падения одинаково для всех тел. Напомним, что при решении большинства задач мы будем пользоваться усреднённым значением g:
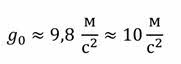
Также в некоторых районах Земли ускорение свободного падения отличается от приведённого среднего значения из-за неоднородного строения земной коры и недр, наличия горных массивов и впадин, а также залежей полезных ископаемых. Там, где имеются залежи более плотных пород (например, металлических руд), значение ускорения свободного падения больше среднего значения, а если залежи лёгких полезных ископаемых (таких, как нефть или газ), то оно меньше среднего значения. Метод определения залежей полезных ископаемых по измерению ускорения свободного падения используется геологами и носит название гравиметрической разведки.
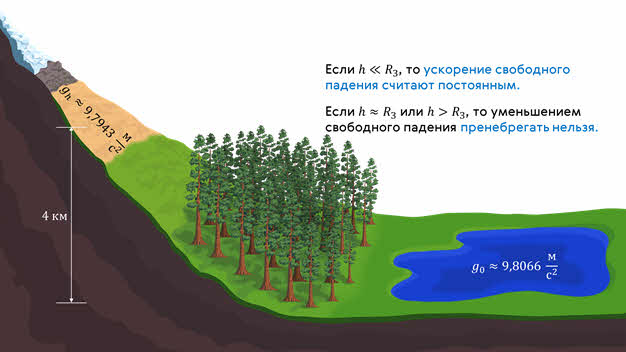
И, как мы уже упоминали, ускорение свободного падения зависит от высоты над уровнем моря — чем больше высота, тем меньше значение «Жэ» и тем меньше сила тяжести, действующая на тело. Вблизи поверхности Земли это уменьшение невелико. Так, например, при подъёме на 4 километра, ускорение свободного падения уменьшается всего на 0,13 %. Поэтому, если высота подъёма тела много меньше радиуса Земли, ускорение свободного падения считают постоянным, пренебрегая его небольшим уменьшением. Но при высоте, сравнимой с радиусом Земли и больше, уменьшением свободного падения пренебрегать нельзя.
Для примера, давайте с вами определим ускорение, вызванное силой тяготения, на высоте, равной двум радиусам Земли от поверхности Земли, если на её поверхности оно равно 9,81 м/с2.

Таким образом видим, что действительно на больших высотах изменение значения ускорения свободного падения очень существенно.
Все вы знаете, что гравитационное поле Солнца «управляет» движением почти всех тел Солнечной системы. Силу тяжести, действующую на тело вблизи поверхности каждой из восьми планет Солнечной системы, можно рассчитать по известной формуле:
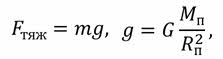
где g — это ускорение свободного падения на исследуемой планете. Конечно оно будет зависеть от массы планеты и её радиуса. Так как массы и радиусы планет известны, то можно подсчитать ускорение свободного падения на каждой из них.
Для примера, определим ускорение свободного падения на самой большой планете нашей солнечной системы — Юпитере, если его масса равна 1,9 ∙ 1027 кг, а радиус — 6,99 ∙ 107 м.

Домашняя работа
стр. 66 — 68
упр. 16