На прошлых уроках мы видели, что положение тела в пространстве всегда определяется относительно какого-то другого тела — тела отсчёта. Для этого с телом отсчёта связывается система координат и выбирается способ измерения времени.
Так как тело отсчёта мы можем выбирать совершенно произвольно, то положение одного и того же тела можно одновременно рассматривать в разных системах координат.
Например, положение самолёта можно определить, указав, что он находится на высоте 10 километров над уровнем моря. Одновременно с этим мы можем сказать, что он находится на высоте 3 километров от вершины горы. Это значит, что положение самолёта относительно: оно различно относительно различных систем отсчёта.

Но относительно не только положение тела, относительно и его движение. В повседневной жизни мы часто встречаемся с ситуациями, в которых одни тела движутся относительно других движущихся тел. Например, пассажир перемещается по вагону движущегося поезда или катер пересекает реку с быстрым течением.

Наконец наша планета вращается вокруг Солнца, которое, в свою очередь, движется к границе созвездий Геркулеса и Лиры со скоростью 20 км/с. Можно привести ещё много таких примеров. И сегодня мы с вами узнаем, каковы закономерности таких движений?
Для начала проведём такой опыт. Опустим металлический шарик в заполненную сахарным сиропом стеклянную трубку, и будем перемещать трубку относительно школьной доски в горизонтальном направлении, не меняя ориентации трубки. Наблюдая за движением шарика, будем отмечать на доске его положения, например, через каждые 10 секунд.
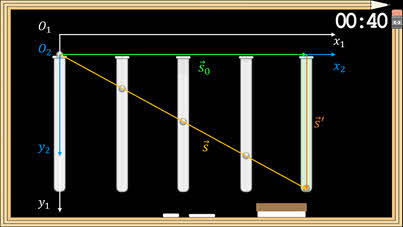
Назовём систему отсчёта, связанную с доской, неподвижной, а систему отсчёта, связанную с трубкой, — движущейся.

Из проведённого опыта видно, что относительно трубки, то есть движущейся системы отсчёта, шарик совершил некоторое перемещение, которое мы обозначим через s’. Сама же подвижная система отсчёта за это время совершила перемещение s0 относительно доски.
Из полученного рисунка видно, что перемещение шарика относительно неподвижной системы отсчёта, равно векторной сумме перемещений:
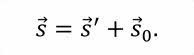
Таким образом, на основании проведённого опыта, мы можем утверждать, что перемещение тела относительно неподвижной системы отсчёта равно векторной сумме его перемещения относительно движущейся системы и перемещения движущейся системы отсчёта относительно неподвижной.
В этом состоит установленный экспериментально принцип независимости движений.
Очевидно, что в нём речь идёт о перемещениях, произошедших за один и тот же промежуток времени. Поэтому давайте разделим каждое из перемещений, на него:
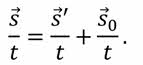
Вектор s/t — это скорость шарика относительно неподвижной системы отсчёта (то есть школьной доски). Вектор s’/t — это скорость движения шарика относительно трубки — подвижной системы отсчёта. А вектор s0/t — это скорость, с которой трубка движется относительно школьной доски.
Таким образом получаем, что скорость тела относительно неподвижной системы отсчёта равна векторной сумме его скорости относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной:
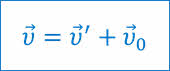
Данное утверждение называется законом сложения скоростей Галилея. Он справедлив не только для равномерного движения, но и для тел, движущихся с ускорением. В этом случае векторы скорости — это мгновенные скорости тел.
Закон сложения скоростей используется при решении многих практически важных задач. Он позволяет, например, найти скорость снаряда, выпущенного из движущегося танка, или скорость самолёта, заходящего на посадку при сильном ветре.

Но следует помнить, что закон сложения скоростей применим только для тел, движущихся со скоростями, во много раз меньшими, чем скорость света.
Мы уже знаем, что траектория движения тела в различных системах отсчёта различна (вспомните опыт с вращающимся диском).

Или вот ещё пример. Вам известно, что, например, точка пропеллера вертолёта, летящего над Землёй, описывает окружность в системе отсчёта, связанной с вертолётом. Но для наблюдателя, находящегося на Земле, эта точка движется по винтовой линии. То есть траектория движения тела относительна. А так как путь — это длина траектории, то он также является величиной относительной.
Таким образом, относительность движения проявляется в том, что скорость, траектория, путь, перемещение и некоторые другие характеристики движения относительны, то есть они различны в разных системах отсчёта.