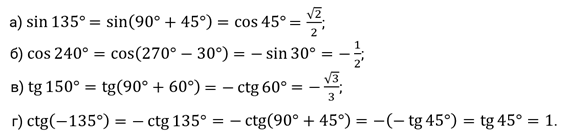Прежде, чем приступить к рассмотрению новой темы, вспомним формулы сложения для синуса: 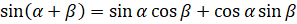 ,
, 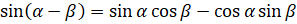 ; косинуса:
; косинуса: 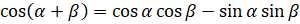 ,
, 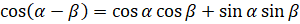 ; тангенса:
; тангенса: 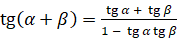 ,
, 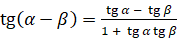 ; котангенса:
; котангенса: 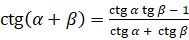 ,
, 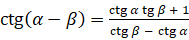 . Также вспомним, если угол
. Также вспомним, если угол 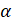 можно представить как
можно представить как 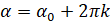 , где
, где 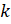 – целое число, то при повороте на угол
– целое число, то при повороте на угол 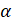 получаем ту же самую точку, что и при повороте на угол
получаем ту же самую точку, что и при повороте на угол 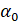 .
.
Вы, наверное, обращали внимание, что таблицы значений синуса, косинуса, тангенса и котангенса обычно составляются для углов от 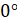 до
до 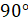 (или от
(или от 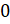 до
до  ). Это означает, что вычисления их значений для остальных углов сводятся к вычислению значений для острых углов.
). Это означает, что вычисления их значений для остальных углов сводятся к вычислению значений для острых углов.
Давайте вычислим 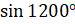 и
и 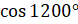 .
.
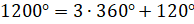 , а значит, при повороте точки
, а значит, при повороте точки 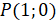 вокруг начала координат на
вокруг начала координат на 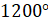 точка совершает три полных оборота и ещё поворот на
точка совершает три полных оборота и ещё поворот на 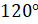 и оказывается в точке
и оказывается в точке 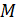 . Таким образом, получается та же самая точка, что и при повороте на угол
. Таким образом, получается та же самая точка, что и при повороте на угол 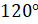 . Тогда можем записать, что
. Тогда можем записать, что 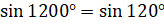 и
и 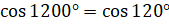 .
.
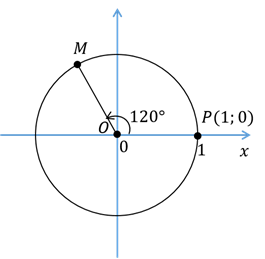
Теперь построим точку 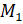 , симметричную точке
, симметричную точке 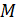 относительно оси
относительно оси 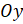 .
.
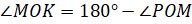 , то есть
, то есть 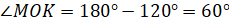 . А так как по построению точки
. А так как по построению точки 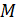 и
и 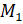 симметричны относительно оси
симметричны относительно оси 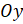 , то и
, то и 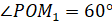 .
.
Тогда 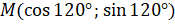 ,
, 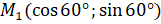 . Точки
. Точки 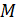 и
и 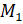 симметричны относительно оси
симметричны относительно оси 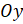 , а значит, их ординаты равны, а абсциссы противоположны по знаку. Можем записать, что
, а значит, их ординаты равны, а абсциссы противоположны по знаку. Можем записать, что 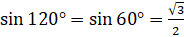 , а
, а 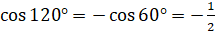 .
.
При решении данной задачи мы выяснили, что 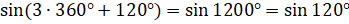 ,
, 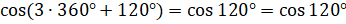
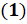 . Эти равенства являются верными, так как при повороте точки
. Эти равенства являются верными, так как при повороте точки 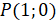 на угол на угол
на угол на угол 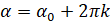 ,
, 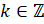 получается та же самая точка, что и при повороте на угол
получается та же самая точка, что и при повороте на угол 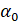 . Тогда справедливы следующие формулы:
. Тогда справедливы следующие формулы: 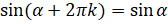 ,
, 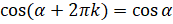 ,
, 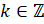
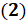 .
.
Также при решении задачи мы получили, что 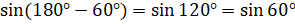 ,
, 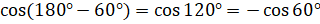
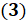 . Эти равенства являются частными случаями формул:
. Эти равенства являются частными случаями формул: 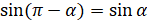 ,
, 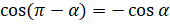
 . Давайте докажем эти формулы.
. Давайте докажем эти формулы.
Итак, докажем формулу 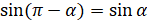 . Применим к левой части формулу
. Применим к левой части формулу 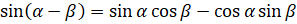 :
: 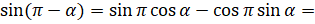 [подставим значения
[подставим значения 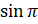 и
и 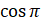 ]
] 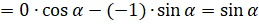 . Формула доказана.
. Формула доказана.
Докажем формулу 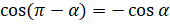 . Для этого применим к левой части формулу
. Для этого применим к левой части формулу 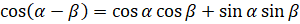 :
: 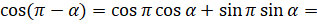 [подставим значения
[подставим значения 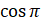 и
и 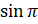 ]
] 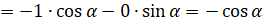 .
.
Доказанные формулы 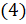 называются формулами приведения. Вообще для синуса формулами приведения являются следующие формулы:
называются формулами приведения. Вообще для синуса формулами приведения являются следующие формулы: 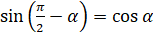 ,
, 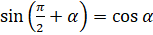 ,
, 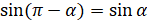 ,
, 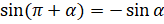 ,
, 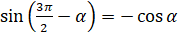 ,
, 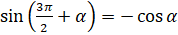
 . Шесть следующих формул являются формулами приведения для косинуса:
. Шесть следующих формул являются формулами приведения для косинуса: 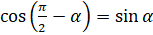 ,
, 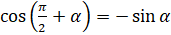 ,
, 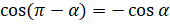 ,
, 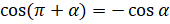 ,
, 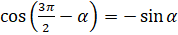 ,
, 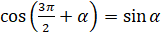
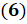 . Отметим, что все эти формулы справедливы при любых значениях
. Отметим, что все эти формулы справедливы при любых значениях 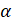 . И каждую из них легко можно доказать с помощью формул сложения для синуса и косинуса аналогично тому, как мы доказали формулы
. И каждую из них легко можно доказать с помощью формул сложения для синуса и косинуса аналогично тому, как мы доказали формулы 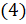 .
.
Давайте вычислим 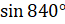 и
и 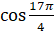 . В первом примере
. В первом примере 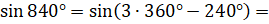 [по первой формуле из формул
[по первой формуле из формул 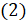 ]
] 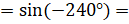 [
[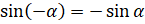 ]
] 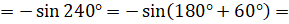 [
[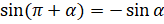 ]
] 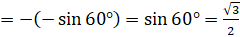 .
.
Вычислим 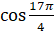 .
. 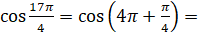 [по второй формуле из формул
[по второй формуле из формул 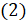 ]
] 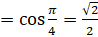 .
.
А есть формулы приведения для тангенса и котангенса? Для тангенса и котангенса тоже есть формулы приведения, то есть вычисление тангенса и котангенса любого угла может быть сведено к вычислению тангенса и котангенса острого угла. Воспользовавшись определением тангенса и формулами 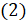 , можем записать, что
, можем записать, что 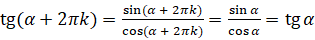 ,
, 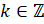 . Теперь запишем
. Теперь запишем 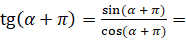 [воспользуемся формулами приведения:
[воспользуемся формулами приведения: 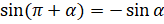 ,
, 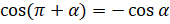 ]
] 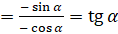 . Следовательно, можем сделать вывод, что
. Следовательно, можем сделать вывод, что 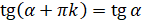 ,
, 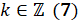 .
.
Аналогичным образом можно доказать, что 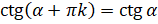 ,
, 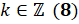 .
.
Следующие формулы являются формулами приведения для тангенса: 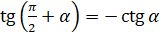 ,
, 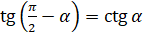
 ; котангенса:
; котангенса: 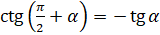 ,
, 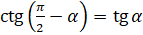
 . Эти формулы имеют место при всех допустимых значениях
. Эти формулы имеют место при всех допустимых значениях 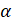 . Чтобы доказать эти формулы, достаточно воспользоваться формулами
. Чтобы доказать эти формулы, достаточно воспользоваться формулами 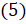 и
и 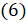 , то есть формулами приведения для синуса и косинуса. Так, например,
, то есть формулами приведения для синуса и косинуса. Так, например, 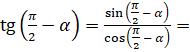 [
[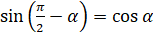 ,
, 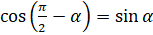 ]
] 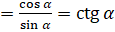 .
.
Таким же образом можно доказать каждую из формул 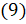 и
и 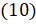 .
.
Давайте вычислим 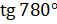 и
и 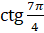 . Итак,
. Итак, 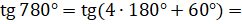 [по формуле
[по формуле 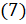 ]
] 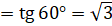 .
.
Теперь вычислим 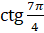 .
. 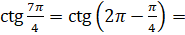 [по формуле
[по формуле 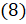 ]
] 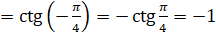 .
.
Отметим, что запоминать формулы приведения совсем не обязательно. Чтобы записать любую из формул, можно применять следующие правила: 1) в правой части формулы ставится тот знак, который имеет левая часть при условии, что 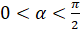 . 2) Если в левой части угол равен
. 2) Если в левой части угол равен 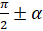 или
или 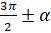 , то синус заменяется на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс. Если угол равен
, то синус заменяется на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс. Если угол равен 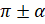 , то замены не происходит. Эти правила облегчают запоминание формул, поэтому их называют мнемоническими правилами.
, то замены не происходит. Эти правила облегчают запоминание формул, поэтому их называют мнемоническими правилами.
Так, например, воспользуемся этими правилами, чтобы записать формулу приведения для выражения 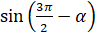 . Если
. Если 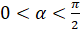 , то
, то 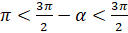 . Синус в третьей четверти принимает отрицательные значения. Тогда по первому правилу в правой части формулы нужно поставить знак «
. Синус в третьей четверти принимает отрицательные значения. Тогда по первому правилу в правой части формулы нужно поставить знак «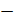 ». В левой части угол равен
». В левой части угол равен 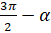 , а значит, по второму правилу синус надо заменить на косинус. Следовательно, получаем, что
, а значит, по второму правилу синус надо заменить на косинус. Следовательно, получаем, что 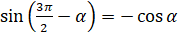 .
.
Рассмотренные формулы 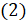 ,
, 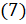 ,
, 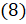 , а также формулы приведения позволяют нам свести вычисление синуса, косинуса, тангенса и котангенса любого угла к вычислению их значений для острого угла.
, а также формулы приведения позволяют нам свести вычисление синуса, косинуса, тангенса и котангенса любого угла к вычислению их значений для острого угла.
А сейчас давайте выполним задание. Вычислите: а) 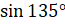 ; б)
; б) 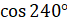 ; в)
; в) 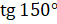 ; г)
; г) 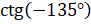 .
.
Решение.