Прежде чем записать уравнение прямой с угловым коэффициентом дадим определения угла наклона прямой к оси Ox и углового коэффициента. Пусть на плоскости задана прямоугольная декартова система координат Oxy.
Определение.
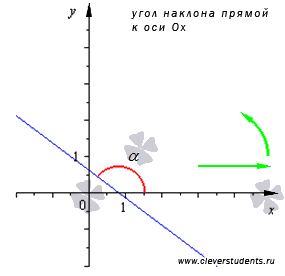
Угол наклона прямой к оси Ox в фиксированной прямоугольной декартовой системе координат Oxy на плоскости — это угол, отсчитываемый от положительного направления оси Ох до прямой против хода часовой стрелки.
 может принимать значения из интервала
может принимать значения из интервала  .
.
Определение.
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.
Угловой коэффициент прямой обычно обозначают буквой k. Тогда по определению 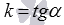 .
.
Если прямая параллельна оси ординат, то угловой коэффициент не существует (в этом случае также говорят, что угловой коэффициент обращается в бесконечность).
Положительный угловой коэффициент прямой указывает на возрастание ее графика функции, отрицательный угловой коэффициент – на убывание. Этой теме посвящена статья нахождение промежутков возрастания и убывания функции.
На рисунке показан угол наклона прямой и указано значение углового коэффициента при различных вариантах расположения прямой относительно прямоугольной системы координат.

Пример.
Найдите угловой коэффициент прямой, если угол ее наклона к оси абсцисс равен  .
.
Решение.
По условию  . Тогда по определению углового коэффициента прямой вычисляем
. Тогда по определению углового коэффициента прямой вычисляем  .
.
Ответ:

Задача нахождения угла наклона прямой к оси абсцисс при известном угловом коэффициенте немного сложнее. Здесь необходимо учитывать знак углового коэффициента. При  угол наклона прямой является острым и находится как
угол наклона прямой является острым и находится как  . При
. При  угол наклона прямой является тупым и его можно определить по формуле
угол наклона прямой является тупым и его можно определить по формуле  .
.
Пример.
Определите угол наклона прямой к оси абсцисс, если ее угловой коэффициент равен 3.
Решение.
Так как по условию угловой коэффициент положителен, то угол наклона прямой к оси Ox острый. Его вычисляем по формуле  .
.
Ответ:

Пример.
Угловой коэффициент прямой равен  . Определите угол наклона прямой к оси Ox.
. Определите угол наклона прямой к оси Ox.
Решение.
Обозначим k – угловой коэффициент прямой,  — угол наклона этой прямой к положительному направлению оси Ox. Так как
— угол наклона этой прямой к положительному направлению оси Ox. Так как  , то используем формулу для нахождения угла наклона прямой следующего вида
, то используем формулу для нахождения угла наклона прямой следующего вида  . Подставляем в нее данные из условия:
. Подставляем в нее данные из условия:  .
.
Ответ:
