На прошлых уроках мы с вами начали изучать прямолинейное равноускоренное движение, то есть движение с постоянным по модулю ускорением. Напомним, что ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости:
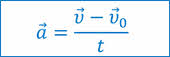
Также мы с вами выяснили, что при равноускоренном движении, скорость тела линейно зависит от времени:

Теперь мы должны выяснить самое главное — как изменяется со временем координата тела при его прямолинейном равноускоренном движении. Для этого, как мы знаем, необходимо знать перемещение тела, так как проекция вектора перемещения как раз и равна изменению координаты тела.
При изучении графического представления равномерного движения мы говорили о том, что проекция перемещения при равномерном движении численно равна площади прямоугольника, ограниченного графиком скорости, осью времени и перпендикулярами к этой оси, восставленными из точек, соответствующих моментам начала и конца наблюдения.
Это же правило применимо и для неравномерного движения. Покажем это. Для чего воспользуемся графиком зависимости проекции скорости от времени. Выберем на графике достаточно малый участок АВ и проведём перпендикуляры из точек А и В» на ось времени:
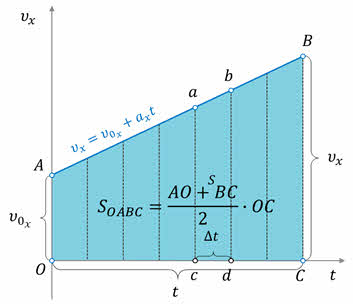
Длина полученного на оси времени отрезка равна тому малому промежутку времени, в течение которого произошло изменение скорости от её значения в точке А, до её значения в точке В. Если этот промежуток времени достаточно мал, то изменением скорости за это время можно пренебречь, то есть движение тела можно считать равномерным. Следовательно, полученная полоска ABCD мало отличается от прямоугольника. А его площадь численно равна проекции перемещения тела за время, соответствующее отрезку CD.
Очевидно, что на такие узкие полоски мы можем разбить всю площадь фигуры под графиком скорости.
Тогда, согласно рисунку, проекция перемещения при равноускоренном движении определяется площадью трапеции. Площадь же трапеции, как известно из геометрии, равна произведению полусуммы её оснований на высоту. В нашем случае длина одного из оснований численно равна проекции начальной скорости тела, другого — проекции скорости через время t, высота же трапеции численно равна времени:
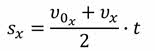
Обратите внимание на первый множитель в уравнении. Мы знаем, что среднее значение проекции скорости равно отношению проекции перемещения тела к промежутку времени, в течение которого это перемещение произошло. Тогда из формулы следует, что средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей:
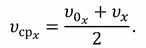
При равноускоренном движении эта формула выполняется не только для проекций, но и для векторов скорости.
Теперь подставим в полученную формулу для проекции перемещения уравнение скорости и, проведя простые математические преобразования, получим формулу, выражающую зависимость проекции перемещения от времени при равноускоренном движении:
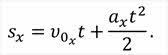
При использовании формулы нужно помнить, что входящие в неё величины могут иметь разные знаки, так как это проекции векторов перемещения, начальной скорости и ускорения.
Учитывая, что проекция перемещения равна разности конечной и начальной координат тела, получим формулу, выражающую кинематический закон равноускоренного движения:
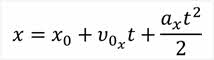
Из полученных формул видим, что при равноускоренном движении проекция перемещения тела и его координата квадратично зависят от времени. В математике квадратичную зависимость записывают в виде
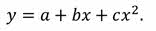
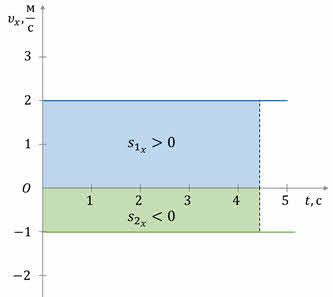
Её график представляет собой параболу, направление ветвей которой зависят от знака коэффициента с. Следовательно, для равноускоренного движения графиком проекций перемещений при равноускоренном движении являются участки парабол, положение вершин которых зависят от направлений начальной скорости и ускорения тела.
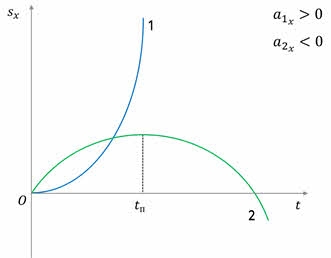
На первом графике проекция перемещения всё время растёт, что соответствует движению с положительным ускорением, а на втором графике — растёт до некоторого момента времени, а затем уменьшается. Так происходит потому, что в этот момент времени скорость тела становится равной нулю и направление движения тела изменяется на противоположное. Поэтому второй график соответствует движению тела с отрицательной проекцией ускорения.
— А каким будет график пути?
Для движения, при котором направление скорости не изменяется, график пути совпадает с графиком проекции перемещения. Если же скорость меняет своё направление, то эти графики совпадают лишь до момента поворота. После поворота проекция перемещения начинает уменьшаться, а путь продолжает расти. Причём он увеличивается ровно на столько, на сколько за то же время уменьшается проекция перемещения.
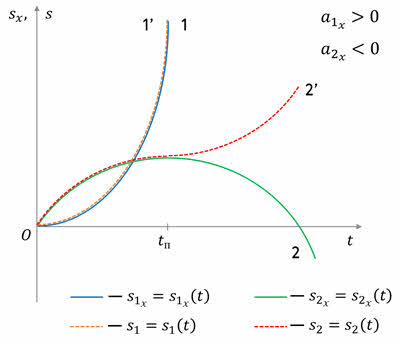
Что касается графика зависимости координаты тела от времени, то он получается из графика проекции перемещения смещением вверх, если начальная координата тела положительна, или вниз, если начальная координата тела отрицательна.

Теперь давайте сравним зависимости основных кинематических величин для двух видов прямолинейного движения:

Как видно из таблицы, если проекция ускорения равна нулю, то формулы равноускоренного движения переходят в формулы равномерного.
Закрепления материала.
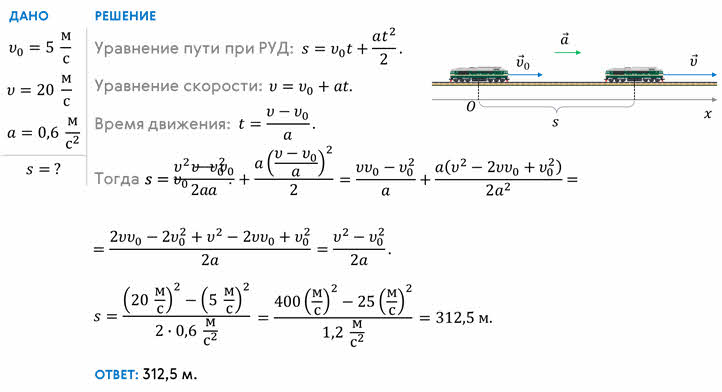
Локомотив двигался со скоростью 5 м/с. Увидев зелёный свет светофора, машинист увеличил скорость, причём ускорение при разгоне составило 0,6 м/с2. Рассчитайте путь, на котором скорость локомотива увеличилась до 20 м/с.
Домашняя работа
Стр. 28 — 31
Упр. №7
Электронный учебник: http://urok55.ru/%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0-9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D1%83%D1%87%D0%B5%D0%B1%D0%BD%D0%B8%D0%BA/