Упражнения.
Задача 1. Железный провод длиной 250 м имеет площадь поперечного сечения 2 мм2. Найдите сопротивление данного провода.

Задача 2. Какое напряжение должно быть на эбонитовом диске толщиной 1 мм, чтобы через него прошел ток в 1 мкА? Диаметр диска составляет 1 см.
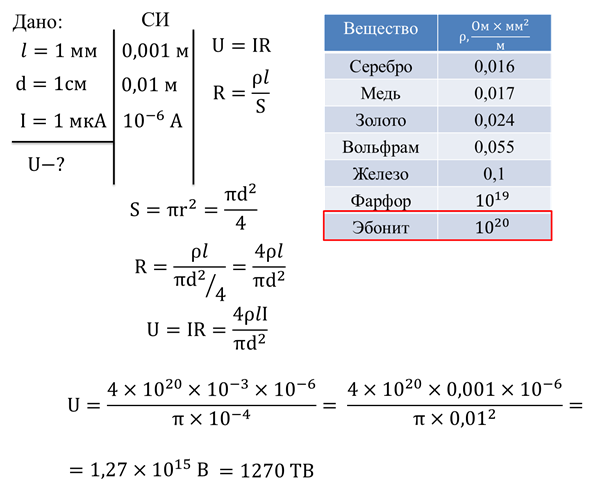
Мы видим, что даже для того, чтобы через эбонит прошел очень маленький ток, нужно просто огромное напряжение. Такое напряжение создать практически невозможно. Даже в современных ускорителях частиц достигалось напряжение не больше нескольких ТВ. Поэтому, можно сказать, что мы не можем провести ток через эбонит. Этого следовало ожидать, поскольку удельное сопротивление эбонита огромно, и он является непроводником.
Задача 3. На рисунке показан график зависимости силы тока на участке цепи от неизвестной величины. Можете ли вы определить, что это за величина?
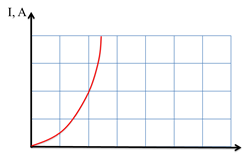
Итак, давайте вспомним, от чего вообще может зависеть сила тока. В первую очередь, сила тока — это количество заряда, прошедшего через поперечное сечение за единицу времени. Из формулы видно, что сила тока находится в линейной зависимости от количества заряда в единицу времени, а на рисунке мы видим график функции, который показывает нелинейную зависимость. Мы знаем, что график функции, описывающий любую линейную зависимость, будет являться прямой. Из формулы, описывающей закон Ома, мы видим, что сила тока прямо пропорциональна напряжению. Значит, неизвестная величина не является ни количеством заряда, ни напряжением. Сила тока обратно пропорциональна сопротивлению. Однако, мы уже знаем, что график функции зависимости силы тока от сопротивления представляет собой ветвь гиперболы, а на рисунке мы видим другой график.
Тогда следует заметить, что сила тока зависит от величин, которые, в свою очередь, зависят от других величин. Напряжение связано с работой по переносу заряда, но эта зависимость тоже линейная. Рассмотрим, от чего зависит сопротивление: от удельного сопротивления, от длины проводника и от площади поперечного сечения. Удельное сопротивление для каждого проводника — есть величина постоянная. Сопротивление находится в линейной зависимости от длины проводника, длина проводника — это независимая величина. Остается площадь поперечного сечения. Как раз-таки, она зависит не от радиуса, а от квадрата радиуса проводника, что приводит нас к нелинейной зависимости. Если мы преобразуем формулу, по которой вычисляется сила тока в проводнике, то увидим, что сила тока прямо пропорциональна квадрату радиуса проводника. Это единственная величина, которая могла привести к построению графика квадратичной функции. Действительно, если мы внимательно изучим график, то убедимся, что это парабола. Следует заметить, что это может быть график зависимости силы тока не от радиуса, а от диаметра. Однако, для того, чтобы это проверить, нам нужна дополнительная информация. Тем не менее, мы с уверенностью можем сказать, что это график зависимости силы тока либо от радиуса, либо от диаметра проводника (по форме эти два графика ничем не отличаются — существуют лишь числовые отличия).
Домашняя работа!
Стр. 131 — 132 читать. Упр. 30