 Загрузка...
Загрузка...
На одном из прошлых уроков мы с вами говорили о том, что заряженные тела взаимодействуют друг с другом посредством особого вида материи, которую называют электрическим полем. Примером такого взаимодействия может служить электрический ток, то есть упорядоченное движение заряженных частиц, которое создаётся электрическим полем.
Интересно, что нам с вами сам по себе электрический ток не нужен. Важным для нас является не сам ток, а его действие. А вот действие электрического тока характеризуется работой электрического тока.
Давайте вспомним, что в общем случае под работой понимают скалярную физическую величину, которая описывает действие силы, приводящее к изменению значения скорости рассматриваемого тела.
Поэтому работа тока — это, говоря строгим языком физики, работа электрически сил, которые, перемещая заряженные частицы, увеличивают их скорость, а значит и кинетическую энергию.
Мы уже с вами знаем, что работа по переносу электрического заряда в электрическом поле оценивается произведением величины перенесённого заряда на величину напряжения между начальной и конечной точками переноса:
A = ΔqU.
Очевидно, что это соотношение может быть применимо и для оценки работы тока. Однако эта формула имеет неудобство в связи с тем, что и ней фигурирует перенесённый в электрическом поле заряд, измерение которого требует особых методов. Поэтому удобнее расписать этот заряд, используя формулу силы тока:
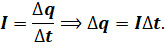
Такая запись приводит нас к удобной формуле для определения работы электрического тока: работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого шёл ток:
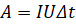 .
.
В этой формуле все величины измеряются известными нам приборами: амперметром, вольтметром и секундомером (хотя в реальной жизни для измерения работы тока мы с вами пользуемся специальными счётчиками электрической энергии, которые сейчас можно увидеть в каждом доме).
Единицей работы тока, как вы догадались, является джоуль:
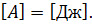
Однако на практике работу тока часто выражают во внесистемных единицах —киловатт-часах:
1 кВт ∙ час = 3,6 ∙ 106 Дж.
Применяя к потребителю электротока закон Ома для участка цепи, можно из основной формулы работы получить ещё два варианта, исключив в первом случае из формулы напряжение, а во-втором — силу тока:
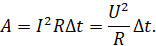
Получив формулу для работы электрического тока, мы легко получим и формулу для мощности тока. Ведь в любом случае мощность находится делением работы на время её совершения:
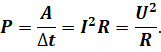
Напомним, что единицей измерения мощности является ватт:
А для измерения мощности электрического тока придумали специальные приборы, которые называются ваттметрами.
Теперь давайте вспомним, что тепловое действие тока проявляется в том, что при протекании тока по проводнику последний нагревается. При этом тепловое действие ток производит в любой среде: твёрдой, жидкой и газообразной.

Давайте вспомним, что нагревание проводника обусловлено тем, что разогнавшиеся под действием электрического поля свободные носители зарядов — электроны — сталкиваются с ионами кристаллической решётки проводника и отдают им часть своей энергии. То есть происходит переход энергии электрического поля во внутреннюю энергию проводника.
При этом, очевидно, что чем больше будет сопротивление проводника, тем большее количество теплоты в нём выделится при протекании электрического тока одной и той же силы.
Это легко проверить на простом опыте. Возьмём три последовательно соединённых проводника, изготовленных из разных материалов, например, из нихрома, никелина и меди, и подключим их к источнику постоянного тока. Спустя некоторое время мы заметим, нихромовый проводник нагрелся почти до белого каления, никелиновый — лишь слегка покраснел, а вот медный проводник практически не изменил свой цвет.
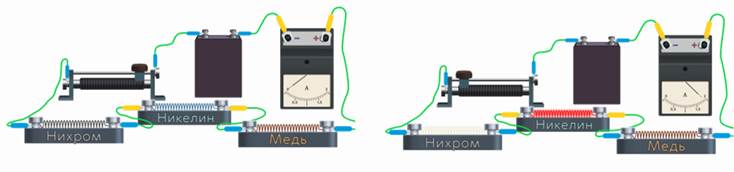
Таким образом, действительно, чем больше сопротивление проводника, тем «труднее» двигаться зарядам в нём и тем больше нагревается проводник.
В 1841 году английский учёный Джеймс Прескотт Джоуль и независимо от него в 1842 году российский учёный Эмилий Христианович Ленц, изучая на опыте тепловые действия тока установили закон, позволяющий рассчитать количество теплоты, выделяемое в проводнике при протекании в нём электрического тока. Согласно этому закону, количество теплоты, выделяющееся в проводнике, прямо пропорционально квадрату силы тока, проходящего по проводнику, сопротивлению проводника и времени, в течение которого поддерживается неизменный ток в проводнике.
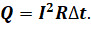
Проверим его справедливость с помощью такого опыта. Возьмём калориметр, содержащий 100 мл воды и поместим в неё проводник в виде спиральки известного сопротивления. Концы проводника включим в цепь, состоящую из источника тока, амперметра и ключа. С помощью секундомера будем засекать время эксперимента.
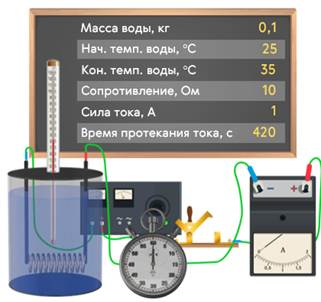
Замкнув ключ, подождём пока температура воды в калориметре не повысится на 10 °С.
Теперь, по известной нам формуле, рассчитаем количество теплоты, полученное водой при нагревании:
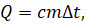
После простых расчётов получаем, что вода получила от нагревателя 4200 Дж теплоты (для простоты расчётов мы пренебрегаем потерями теплоты). Теперь определим количество теплоты, выделившееся в проводнике, используя для этого закон Джоуля — Ленца:
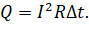
Подставив в полученное уравнение данные наших опытов, найдём, что за время эксперимента в проводнике выделились те же 4200 Дж теплоты. Это подтверждает правоту закона Джоуля — Ленца.