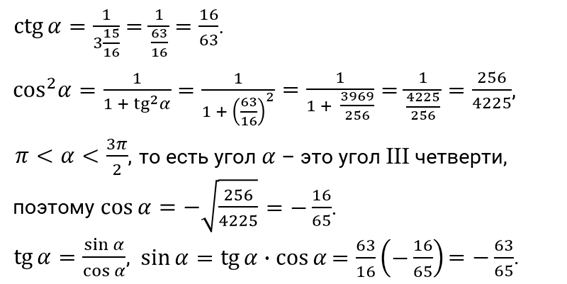Вспомним, что синусом угла 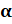 называется ордината точки
называется ордината точки 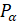 , полученной поворотом точки
, полученной поворотом точки 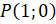 вокруг начала координат на угол
вокруг начала координат на угол 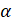 .
.
Косинусом угла 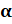 называется абсцисса точки
называется абсцисса точки 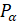 , полученной поворотом точки
, полученной поворотом точки 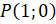 вокруг начала координат на угол
вокруг начала координат на угол 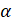 .
.
Тангенсом угла 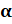 называется отношение синуса угла
называется отношение синуса угла 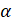 к его косинусу.
к его косинусу.
Котангенсом угла 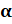 называется отношение косинуса угла
называется отношение косинуса угла 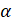 к его синусу.
к его синусу.
Итак, выясним зависимость между синусом и косинусом.
Пусть на координатной плоскости изображена единичная окружность с центром в начале координат. Точка 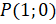 совершает поворот против часовой стрелки на угол
совершает поворот против часовой стрелки на угол 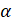 и оказывается в точке
и оказывается в точке 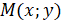 .
.
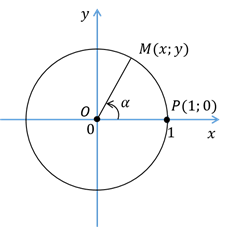
По определению синуса и косинуса можно сказать, что абсцисса точки 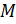 равна косинусу угла поворота, то есть
равна косинусу угла поворота, то есть 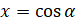 , а ордината точки
, а ордината точки 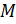 равна синусу угла поворота, то есть
равна синусу угла поворота, то есть 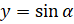 . Тогда можем записать, что точка
. Тогда можем записать, что точка 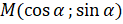 .
.
Теперь вспомним, что уравнение единичной окружности имеет вид: 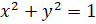 . Так как точка
. Так как точка 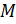 принадлежит нашей единичной окружности, то её координаты удовлетворяют этому уравнению. А значит, можем записать:
принадлежит нашей единичной окружности, то её координаты удовлетворяют этому уравнению. А значит, можем записать: 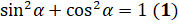 .
.
А как называется это равенство? Это равенство называют основным тригонометрическим тождеством. Оно выполняется при любых значениях 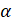 . Основное тригонометрическое тождество часто используется при преобразовании тригонометрических выражений.
. Основное тригонометрическое тождество часто используется при преобразовании тригонометрических выражений.
Давайте из этого тождества выразим 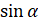 . Итак, перенесём
. Итак, перенесём 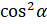 в правую часть равенства:
в правую часть равенства: 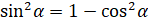 . Извлекаем квадратный корень из обеих частей равенства:
. Извлекаем квадратный корень из обеих частей равенства: 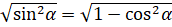 ,
, 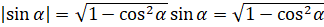 , если
, если 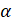 – угол I или II четверти. И
– угол I или II четверти. И 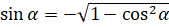 , если
, если 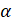 – угол III или IV четверти.
– угол III или IV четверти.
В общем, можем записать так: 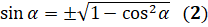 .
.
Теперь выразим 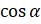 . Перенесём
. Перенесём 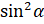 в правую часть равенства:
в правую часть равенства: 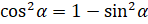 . Извлекаем квадратный корень из обеих частей равенства:
. Извлекаем квадратный корень из обеих частей равенства: 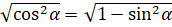 ,
, 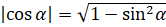 .
. 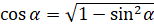 , если
, если 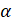 – угол I или IV четверти.
– угол I или IV четверти. 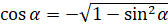 , если
, если 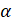 – угол II или III четверти.
– угол II или III четверти.
В общем, можем записать так: 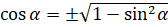
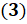 .
.
Вот таким образом мы получили равенства, которые связывают значения синуса и косинуса одного и того же угла.
Давайте вычислим 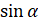 , если
, если 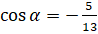 и
и 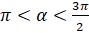 . Воспользуемся формулой
. Воспользуемся формулой 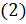 . Так как а
. Так как а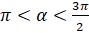 , то есть угол альфа – это угол III четверти, то
, то есть угол альфа – это угол III четверти, то 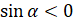 . Поэтому в формуле перед корнем нужно поставить знак «
. Поэтому в формуле перед корнем нужно поставить знак «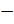 »:
»: 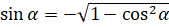 . Тогда подставим значение
. Тогда подставим значение 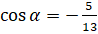 в формулу:
в формулу: 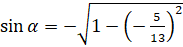 . Выполним вычисления:
. Выполним вычисления: 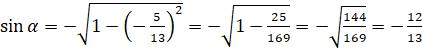 .
.
Теперь давайте вычислим 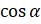 , если
, если 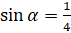 и
и 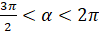 . Воспользуемся формулой
. Воспользуемся формулой 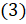 . Так как
. Так как 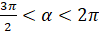 , то есть угол альфа – это угол IV четверти, то
, то есть угол альфа – это угол IV четверти, то 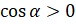 .
.
Поэтому в формуле перед корнем нужно поставить знак «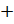 »? Верно. Запишем формулу:
»? Верно. Запишем формулу: 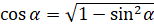 . Подставим значение
. Подставим значение 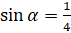 в формулу:
в формулу: 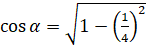 . Выполним вычисления:
. Выполним вычисления: 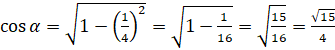 .
.
Ну а теперь выясним зависимость между тангенсом и котангенсом. По определению 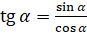 , а
, а 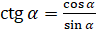 . Перемножим почленно эти равенства:
. Перемножим почленно эти равенства: 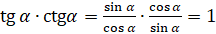 . И получим:
. И получим: 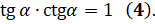 Выразим из этого равенства
Выразим из этого равенства 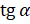 и получим, что
и получим, что 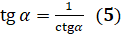 . И выразим
. И выразим 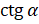 и получим, что
и получим, что 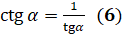 . Важно отметить, что так как на нуль делить нельзя, то
. Важно отметить, что так как на нуль делить нельзя, то 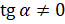 и
и 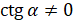 , то есть
, то есть 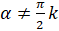 ,
, 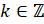 .
.
Вычислим 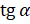 , если
, если 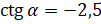 . Подставляем в формулу
. Подставляем в формулу 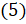 значение котангенса:
значение котангенса: 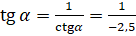 . Вычисляем и получаем
. Вычисляем и получаем 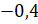 .
.
Вычислим 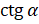 , если
, если 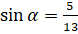 и
и 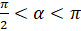 . По формуле
. По формуле 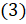 найдём
найдём 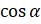 . Так как
. Так как 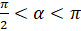 , то есть угол
, то есть угол 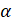 – это угол II четверти, то
– это угол II четверти, то 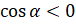 . Поэтому в формуле перед корнем нужно поставить знак «
. Поэтому в формуле перед корнем нужно поставить знак «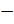 »:
»: 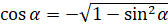 . Подставим значение
. Подставим значение 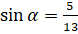 . Выполним вычисления:
. Выполним вычисления: 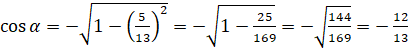 .
.
Теперь найдём значение 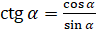 . Подставим значения
. Подставим значения 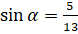 и
и 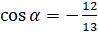 . Выполним вычисления:
. Выполним вычисления:  .
.
И нам осталось найти зависимость между тангенсом и косинусом. Для этого мы с вами разделим обе части основного тригонометрического тождества 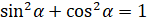 на
на 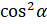 :
: 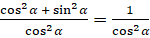 . При этом
. При этом 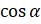 не должен равняться нулю, то есть
не должен равняться нулю, то есть 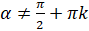 ,
, 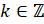 . Преобразуем левую часть равенства:
. Преобразуем левую часть равенства: 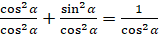 . Первое слагаемое в левой части можем записать как
. Первое слагаемое в левой части можем записать как 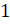 , второе – как
, второе – как 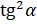 :
: 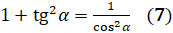 .
.
Эта формула и показывает зависимость между тангенсом и косинусом? Да. Из этой формулы мы можем выразить тангенс через косинус и косинус через тангенс.
Давайте вычислим 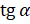 , если
, если 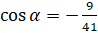 и
и 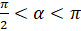 . Выразим
. Выразим 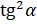 из формулы
из формулы 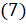 :
: 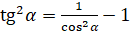 . Подставим значение
. Подставим значение 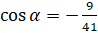 :
: 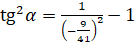 . Выполним вычисления:
. Выполним вычисления: 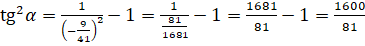 .
. 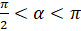 , то есть это угол II четверти. Тангенс во второй четверти принимает отрицательные значения. Поэтому
, то есть это угол II четверти. Тангенс во второй четверти принимает отрицательные значения. Поэтому 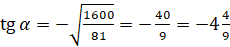 .
.
И вычислим 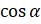 , если
, если 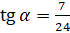 и
и 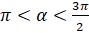 . Из формулы
. Из формулы 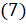 выразим
выразим 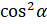 :
: 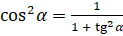 . Подставим значение
. Подставим значение 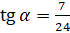 :
: 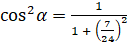 . Выполним вычисления:
. Выполним вычисления: 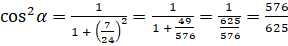 . У нас
. У нас 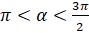 . Косинус в III четверти принимает отрицательные значения. Поэтому
. Косинус в III четверти принимает отрицательные значения. Поэтому 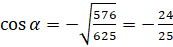 .
.
А сейчас выполним несколько заданий.
Задание первое. Найдите 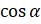 ,
, 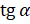 и
и 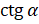 , если
, если 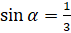 и
и 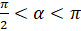 .
.
Решение.
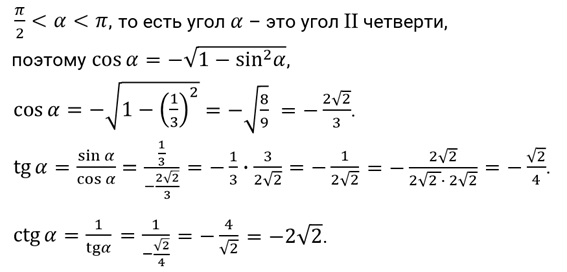
Задание второе. Найдите 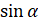 ,
, 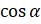 и
и 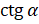 , если
, если 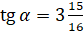 и
и 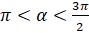 .
.
Решение.