Вспомним, что синусом угла 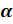 называется ордината точки
называется ордината точки 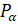 , полученной поворотом точки
, полученной поворотом точки 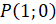 вокруг начала координат на угол
вокруг начала координат на угол 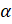 .
.
Косинусом угла 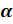 называется абсцисса точки
называется абсцисса точки 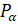 , полученной поворотом точки
, полученной поворотом точки 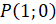 вокруг начала координат на угол
вокруг начала координат на угол 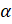 .
.
Тангенсом угла 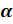 называется отношение синуса угла
называется отношение синуса угла 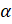 к его косинусу.
к его косинусу.
Котангенсом угла 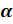 называется отношение косинуса угла
называется отношение косинуса угла 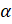 к его синусу.
к его синусу.
Теперь приступим к рассмотрению новой темы. Итак, пусть на координатной плоскости изображена единичная окружность с центром в начале координат. Точка 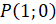 совершает поворот против часовой стрелки на угол
совершает поворот против часовой стрелки на угол 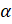 и оказывается в точке
и оказывается в точке 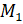 . По определению синуса и косинуса можем сказать, что абсцисса точки
. По определению синуса и косинуса можем сказать, что абсцисса точки 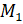 равна
равна 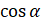 , а ордината –
, а ордината – 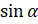 . Затем точка
. Затем точка 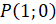 совершает поворот на угол
совершает поворот на угол 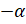 , противоположный углу
, противоположный углу 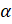 , и оказывается в точке
, и оказывается в точке 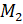 .
.
Тогда абсцисса точки 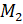 равна
равна 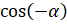 , а ордината равна
, а ордината равна  ? Верно.
? Верно.
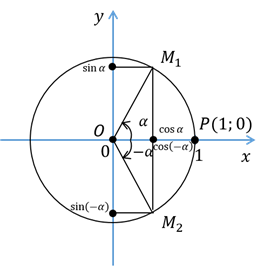
Посмотрите на угол 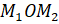 . Ось
. Ось 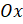 делит его пополам, а значит, точки
делит его пополам, а значит, точки 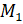 и
и 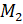 симметричны относительно оси
симметричны относительно оси 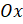 .
.
Тогда абсциссы этих точек совпадают, а ординаты имеют противоположные значения, то есть можем записать, что 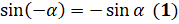 , а
, а 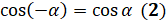 . Сразу отметим, что формулы
. Сразу отметим, что формулы 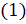 и
и 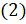 справедливы при любых значениях
справедливы при любых значениях 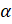 .
.
А что можно сказать про тангенс противоположных углов? По определению тангенса угла можем записать, что 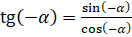 . По формуле
. По формуле 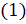 числитель запишем как
числитель запишем как 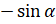 , по формуле
, по формуле 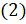 знаменатель запишем как
знаменатель запишем как 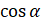 :
: 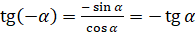 . Таким образом, мы получили, что
. Таким образом, мы получили, что 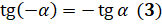 . Отметим, что здесь
. Отметим, что здесь 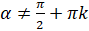 ,
, 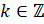 , так как ранее мы с вами говорили, что тангенс этих углов не определён.
, так как ранее мы с вами говорили, что тангенс этих углов не определён.
Как быть с котангенсом противоположных углов? По определению котангенса угла запишем: 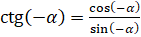 . По формуле
. По формуле 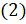 числитель запишем как
числитель запишем как 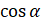 , а знаменатель по формуле
, а знаменатель по формуле 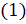 запишем как
запишем как 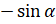 :
: 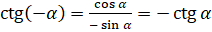 . Таким образом, получили, что
. Таким образом, получили, что 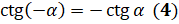 . Здесь
. Здесь 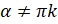 ,
, 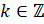 , так как котангенс этих углов не определён.
, так как котангенс этих углов не определён.
Полученные формулы позволяют перейти от вычисления синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов.
Давайте найдём 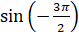 ,
, 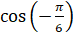 ,
, 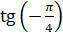 ,
, 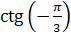 .
.
Итак, вычислим 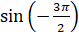 . Воспользуемся формулой
. Воспользуемся формулой 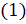 и запишем
и запишем 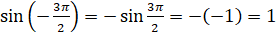 .
.
По формуле 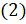 :
: 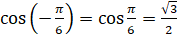 .
.
По формуле 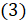 :
: 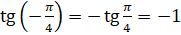 .
.
И вычислим 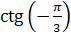 . Воспользуемся формулой
. Воспользуемся формулой 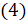 и запишем
и запишем 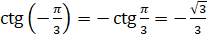 .
.
А теперь выполним несколько заданий.
Задание первое. Вычислите: а) 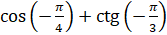 ; б)
; б) 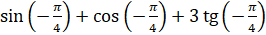 ; в)
; в) 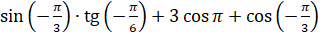 ; г)
; г) 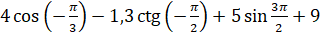 .
.
Решение.
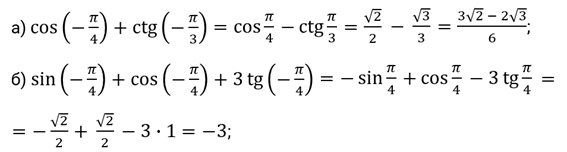
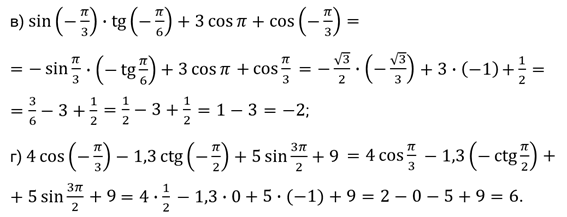
Второе задание. Упростите выражения: а) 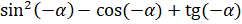 ; б)
; б) 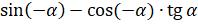 ;
; 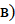
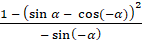 .
.
Решение.
