Пример 1. Переведите число 101,011 из двоичной системы в десятичную.
- Каждый разряд исходного числа умножим на его основание в степени n, где n – номер разряда, при этом 0 – самый младший целый разряд.
- Для дробных разрядов n — отрицательный.
- Сложим полученные значения.
Пример 2. Переведите число 105,4 из восьмеричной системы в десятичную.
Пример 3. Переведите число 29A,516 в десятичную систему счисления.
29A.51616 = (2 × 162) + (9 × 161) + (10 × 160) + (5 × 16-1) + (1 × 16-2) + (6 × 16-3) = 512 + 144 + 10 + 0.3125 + 0.00390625 + 0.00146484375 = 666.3178710937510
Пример 4. Переведите десятичное число 0,816 в двоичную систему с точностью до десятитысячных.
- Умножаем дробную часть на основание искомого числа и записываем полученную в результате умножения целую часть.
- Повторяем операцию с дробной частью полученного числа до тех пор, пока не получится целое число, либо до необходимого количества знаков после запятой.
- Записываем полученные значения сверху вниз.
| Умножение | Результат | Целая часть | Остаток |
|---|---|---|---|
| 0.816 × 2 | 1.632 | 1 | 0.632 |
| 0.632 × 2 | 1.264 | 1 | 0.264 |
| 0.264 × 2 | 0.528 | 0 | 0.528 |
| 0.528 × 2 | 1.056 | 1 | 0.056 |
Пример 5. Перевести данное число 380,1875 из десятичной системы счисления в двоичную.
- Делим исходное число на основание искомого числа и записываем остаток до тех пор, пока неполное частное не будет равно нулю.
- Полученные остатки записываем в обратном порядке.
| Деление | Целое частное | Остаток |
|---|---|---|
| 380 ÷ 2 | 190 | 0 |
| 190 ÷ 2 | 95 | 0 |
| 95 ÷ 2 | 47 | 1 |
| 47 ÷ 2 | 23 | 1 |
| 23 ÷ 2 | 11 | 1 |
| 11 ÷ 2 | 5 | 1 |
| 5 ÷ 2 | 2 | 1 |
| 2 ÷ 2 | 1 | 0 |
| 1 ÷ 2 | 0 | 1 |
- Умножаем дробную часть на основание искомого числа и записываем полученную в результате умножения целую часть.
- Повторяем операцию с дробной частью полученного числа до тех пор, пока не получится целое число, либо до необходимого количества знаков после запятой.
- Записываем полученные значения сверху вниз.
| Умножение | Результат | Целая часть | Остаток |
|---|---|---|---|
| 0.1875 × 2 | 0.375 | 0 | 0.375 |
| 0.375 × 2 | 0.75 | 0 | 0.75 |
| 0.75 × 2 | 1.5 | 1 | 0.5 |
| 0.5 × 2 | 1 | 1 |
Ответ: 380.187510 = 101111100.00112
Пример 6. Сложить два двоичных числа 1012, 112
| +1 | +1 | +1 | |
| + | 1 | 0 | 1 |
| 1 | 1 | ||
| 1 | 0 | 0 | 0 |
| 1 + 1 = 10 |
| 0 пишем, 1 переносим |
| 0 + 1 + 1 = 10 |
| 0 пишем, 1 переносим |
| 1 + 1 = 10 |
Пример 7. Из двоичного числа 1012 вычесть двоичное число 112.
| -1 | |||
| — | 1 | 0 | 1 |
| 1 | 1 | ||
| 0 | 1 | 0 |
| 1 — 1 = 0 |
| 0 меньше 1 поэтому занимаем 1 в старшем разряде. |
| 10 — 1 = 1 |
| 1 -1 = 0 |
| Конец расчета. |
Пример 8. Умножить двоичные числа 1012 и 112.
| x | 1 | 0 | 1 | ||
| 1 | 1 | ||||
| + | 1 | 0 | 1 | ||
| 1 | 0 | 1 | |||
| 1 | 1 | 1 | 1 |
| 1 * 1 = 1 |
| 0 * 1 = 0 |
| 1 * 1 = 1 |
| 1 * 1 = 1 |
| 0 * 1 = 0 |
| 1 * 1 = 1 |
Пример 9. Разделить число 1012 на 112.
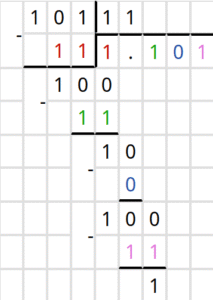
| Делим нацело 101 / 11 = 1 |
| 1 * 11 = 11 |
| 101 — 11 = 10 |
| Так как достигнут конец делимого, а остаток не ноль, то ставим точку в частное и продолжаем деление. |
| Делим нацело 100 / 11 = 1 |
| 1 * 11 = 11 |
| 100 — 11 = 1 |
| Делим нацело 10 / 11 = 0 |
| 0 * 11 = 0 |
| 10 — 0 = 10 |
| Делим нацело 100 / 11 = 1 |
| 1 * 11 = 11 |
| 100 — 11 = 1 |
| Конец расчета. |
Пример 10. Найдите основания системы счисления, если известно, что 23x=1510
Решение:
Так как мы переводим из какой-то системы счисления в десятичную, то
перевод будет выглядеть следующим образом:
2*х1+3*х0=15
2х+3=15
2х=12
х=6
Ответ: 6.
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |