На прошлом уроке мы с вами говорили о многоугольниках. Напомним, что многоугольником называется геометрическая фигура, которая состоит из отрезков и внутренней области. Точки A1, A2, A3 и т.д., An-1, An называют вершинами многоугольника, а отрезки A1A2, A2A3,…, An-1An, An называют сторонами многоугольника.
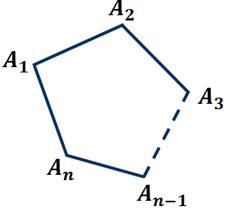
Многоугольник с n вершинами называют n-угольником.
На этом уроке мы поговорим о четырёхугольниках. Итак, четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.
При этом никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
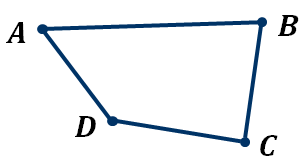
Точки A, B, C и D называются вершинами четырёхугольника. А отрезки AB, BC, CD и DA, соединяющие эти точки называются сторонами четырёхугольника.
Давайте посмотрим на следующие фигуры.
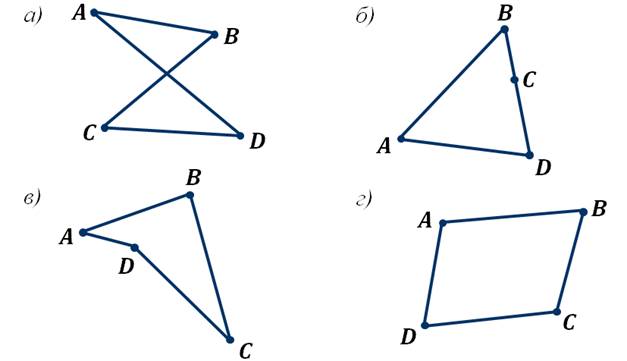
Каждая фигура состоит из четырёх точек и четырёх отрезков, которые последовательно соединяют эти точки. Но обратите внимание, что у первой фигуры отрезки AD и BC пересекаются, а, следовательно, она не является четырёхугольником. У следующей фигуры точки B, C и D лежат на одной прямой, а значит, она также не является четырёхугольником. Следующая фигура является четырёхугольником, так как у неё никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются. И последняя фигура также является четырёхугольником, так как никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
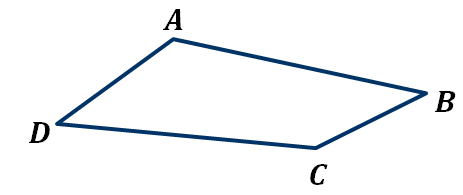
Вершины четырехугольника, принадлежащие одной стороне, называются соседними. Например, вершины A и B, А и D являются соседними.
Вершины, которые не являются соседними, называются противоположными. Так в нашем четырёхугольнике вершины А и C, B и D являются противоположными.
Стороны четырёхугольника, исходящие из одной вершины, называются соседними. Например, стороны BC и CD являются соседними.
Стороны, не имеющие общего конца, называются противоположными. Так стороны AB и CD, AD и BC являются противоположными.
Четырёхугольники бывают выпуклыми и невыпуклыми.
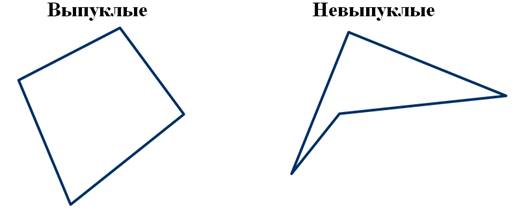
Выпуклый четырёхугольник лежит по одну сторону от прямой, проходящей через любые две соседние вершины. А вот если четырёхугольник лежит по разные стороны хотя бы от одной прямой, проходящей через две соседние вершины, то он является невыпуклым.
Отрезки, соединяющие противоположные вершины четырёхугольника, называются диагоналями.
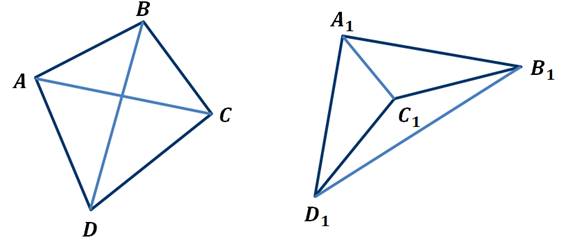
Так в выпуклом четырёхугольнике ABCD отрезки AC и BD являются диагоналями. Каждая диагональ разделяет этот четырёхугольник на два треугольника.
В невыпуклом четырёхугольнике A1B1C1D1 отрезки A1C1 и B1D1 являются диагоналями. И диагональ A1C1 разбивает этот четырёхугольник на два треугольника.
Периметром четырёхугольника называется сумма длин всех его сторон.
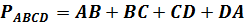
Теперь вспомнив, что сумма углов выпуклого н-угольника равна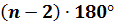 
, легко можем найти сумму углов выпуклого четырёхугольника. Для этого в данное выражение вместо n подставим 4, так как четырёхугольник имеет 4 угла, выполним вычисления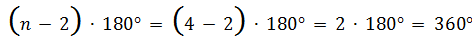
и получим 360º. То есть сумма углов выпуклого четырёхугольника равна трёмстам шестидесяти градусам.
Давайте решим несколько задач.
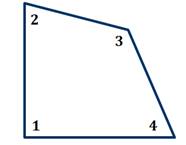
Задача. На рисунке изображён выпуклый четырехугольник, у которого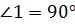 
, 
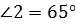, а 
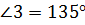. Найдите градусную меру 
.
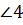Решение. Выше мы выяснили, что сумма углов выпуклого четырёхугольника равна 360º. А тогда может составить следующее равенство: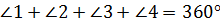 
.
Теперь подставив в это равенство известные градусные меры углов, получим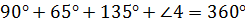 
. Выразим угол 4: 
.
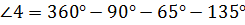Таким образом получили, что градусная мера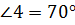 
.
Ответ: 70º.
Задача. Найдите стороны четырёхугольника, если его периметр равен 66 см. Сторона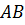 
больше стороны 
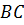на 8 см и на столько же меньше стороны 
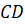, а сторона 
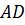в три раза больше стороны .
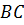Решение.
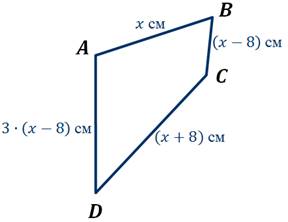
Обозначим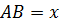 
см, тогда 
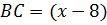см,
см,
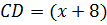см.
.
,
,
,
,
,
.
(см), 
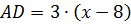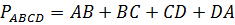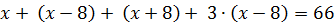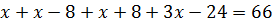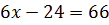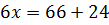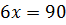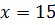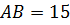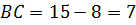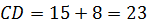(см),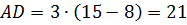
(см),
(см).
Ответ: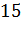 
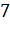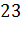см, 
см,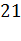 
см, 
см.
Пройдите тест
