Материалы урока
Давайте представим себе такую историю…
– 2, 0, 1, 7, 2, 0, 1, 7, 2, 0, 1, – бурчал себе под нос Саша.
– Чем это ты тут занимаешься? – спросил Паша.
– Хочу научиться красиво писать цифры, – ответил Саша.

– Саша, смотри, какое интересное число у тебя получилось, – провозгласил Паша.
– А ты можешь его прочитать? – спросил он у Саши.
– Прочитать! Конечно! – взбодрился Саша. – Что тут сложного? 2, 0, 1, 7, 2, 0…
– Нет, Саша! – перебил Паша. – Ты просто перечисляешь записанные цифры, а назвать число – это совсем по-другому. Вот как ты думаешь, что общего между буквами и цифрами?
– Не знаю, – прозвучал ответ Саши. – Может, только если одни и другие мы учим в школе?
– Ну почти! – сказал Паша. – Буквы и цифры – это знаки, которые придумали для записи. Так, например, из букв можно записать слово, а вот из цифр – число. У тебя из цифр тоже получилось число, которое имеет своё имя.

– Правда? – удивился Саша. – И как же его зовут?
– Ты знаешь, я немного забыл, как правильно его назвать, – стушевался Паша. – Но я точно знаю, кто нам может помочь!
– Ребята, прежде, чем я вам поведаю свой рассказ о цифрах, числах и ещё кое о чём интересном, хочу, чтобы вы немного размялись и выполнили устные задания, – предложил Электроша.
– Давайте сверимся! – сказал Электроша. – Посмотрите, что у вас должно было получиться!

– Ну а теперь давайте поговорим о числах, – предложил Электроша. – Вы уже знаете, что в алфавите русского языка существует 33 буквы и из них можно составить огромное множество слов.

Цифры в математике выполняют такую же роль, как и буквы в русском языке. Только из цифр составляют различные числа.

Правда, цифр гораздо меньше, чем букв. Их всего лишь 10:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
– Так мало? –удивился Саша.

– Цифр-то мало, а вот составить из них чисел можно сколько угодно! – продолжил Электроша.
– А вы знаете, что цифры изобрели давным-давно? – спросил у мальчиков Электроша. Это произошло в Индии ещё в VI веке. Правда, сами цифры принято называть арабскими.

– Арабскими? – удивился Паша. – Но ведь ты же сказал, что цифры придумали в Индии? А значит, их нужно называть индийскими!
– Всё правильно Паша! – улыбнулся Электроша, – придумали то их в Индии, но к нам цифры пришли от арабов, которые подсмотрели их у индийцев, поэтому-то их и стали называть арабскими.

– А теперь поговорим о том, как называют числа! – продолжил Электроша. От количества цифр (знаков) в числе зависит его название. Так, например, если число состоит из одной цифры, то его называют однозначным.
– Такое смешное название! – ухмыльнулся Саша.
– Да, да, одна цифра – один знак, поэтому и однозначное, – продолжил Электроша. –Самое маленькое однозначное натуральное число – 1, а самое большое – 9.
Кроме однозначных чисел, есть и многозначные. Если число состоит из двух цифр, то его называют двузначным числом.
– Вот вы, мальчики, можете назвать самое маленькое и самое большое двузначное натуральное число? – спросил Электроша.
– Конечно! – обрадовались мальчишки. – Это же легче лёгкого!
– Самое маленькое двузначное число – это 10, – сказал Паша.
– Верно! – подтвердил Электроша.
– А вот самое большое двузначное число – это 90! – воскликнул Саша.
– Нет, нет, – исправил Сашу Электроша. Самое большое двузначное число – 99. А вот следом за ним уже идёт наименьшее трёхзначное натуральное число – 100. Число сто записано тремя цифрами, поэтому его называют трёхзначным.

Запомните! Многозначное число может начинаться с любой цифры, кроме цифры ноль.
Каждая цифра в записи многозначного числа занимает определённое место – позицию.
– Что это значит – определённое место? – решил спросить Саша.
– Перед вами три трёхзначных числа, – продолжил Электроша. – Посмотрите: в их записи участвуют одни и те же цифры.
– Но ведь сами числа же различны, – возразил Паша. – В них цифры стоят на разных местах.

– Ты правильно заметил, Паша, – сказал Электроша. – В записи числа важно то, какую позицию занимает цифра, то есть на каком месте она стоит.
Место, на котором стоит цифра в записи числа, по-другому называют разрядом числа. Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.

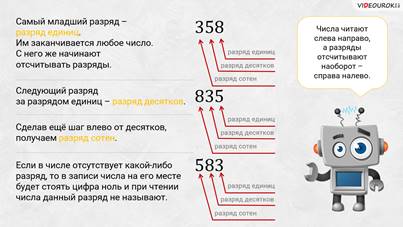
– Да, да, я вспомнил, – радостно сказал Паша, – нам в школе рассказывали. Вот если взять, например, число 358, то у него цифра 8 относится к разряду единиц, цифра 5 – к разряду десятков, а вот цифра 3 – к разряду сотен.
– Всё правильно, Паша! – подбодрил мальчика Электроша. Самый младший разряд – разряд единиц. Им заканчивается любое число. С него же начинают отсчитывать разряды.
Обратите внимание: числа читают слева направо, а разряды отсчитывают наоборот – справа налево. Итак, первый – это разряд единиц. Следующий за ним разряд – разряд десятков. Сделав ещё шаг влево от десятков, получаем разряд сотен.
Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра 0 и при чтении числа данный разряд не называют.
– Мы с Сашей хотели прочитать число, которое у него получилось, – перебил Паша. – Посмотри, какое большущее число у него вышло.
– Ребята, прочитать это число совсем не сложно, – сказал Электроша. – Сейчас я вам покажу, как это сделать.
Итак, чтобы прочитать многозначное число, цифры его записи нужно мысленно разбить справа налево на группы по три цифры в каждой, при этом крайняя слева группа цифр может состоять необязательно только из трёх цифр, в ней могут быть две, как в нашем числе, или даже одна цифра. Эти группы называют классами.

– Классами? – уточнил Саша. Ты ничего не путаешь, Электроша? В классах учатся в школе. Числа же не учатся в школе.
– Именно классами! – улыбнулся Электроша. – Многозначные числа разбивают на классы для удобства их чтения и записи. Единицы, десятки, сотни образуют первый класс – класс единиц. Следующие три цифры числа образуют соответственно разряды: единицы тысяч, десятки тысяч, сотни тысяч. Единицы тысяч, десятки тысяч и сотни тысяч образуют второй класс – класс тысяч. Если мы продвинемся ещё дальше влево, то обнаружим ещё три разряда: единицы миллионов, десятки миллионов и сотни миллионов. Единицы миллионов, десятки миллионов, сотни миллионов образуют третий класс – класс миллионов. Следующие три цифры числа образуют соответственно разряды: единицы миллиардов, десятки миллиардов и сотни миллиардов, а вместе они составляют четвёртый класс – класс миллиардов.

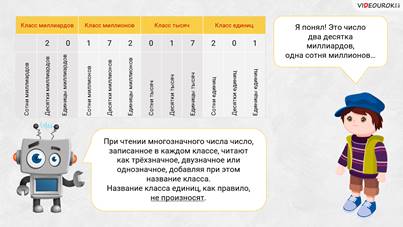
– Я понял, как назвать моё число! – вскрикнул Саша. – Это число два десятка миллиардов, одна сотня миллионов…
– Нет, Саша! – перебил мальчика Электроша. – Ты не до конца понял.
При чтении многозначного числа число, записанное в каждом классе, читают как трёхзначное, двузначное или однозначное, добавляя при этом название класса. Только вот название класса единиц, как правило, не произносят.
– А, понятно, – обрадовался Саша. – Значит, в моём числе 20 миллиардов?
– Правильно! – сказал Электроша. – Может, ты сможешь назвать всё число?
– Я попробую, – ответил Саша. – Моё число, – продолжил он, – можно прочитать так: 20 миллиардов 172 миллиона 17 тысяч 201.
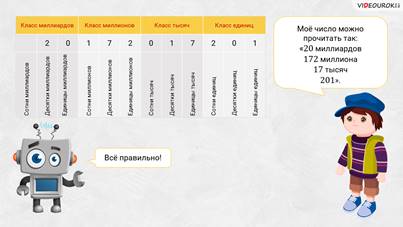
– Всё правильно, Саша! – сказал Электроша. – С чтением многозначного числа ты справился на отлично. Ещё вам с Пашей полезно будет узнать, как правильно записывать многозначные числа.
Чтобы записать многозначное число, вам пригодятся следующие правила:
1. Многозначные числа записывают слева направо и начинают со старшего разряда.
2. Во всех классах, кроме старшего, должно быть по три цифры.
3. Для удобства чтения между классами можно оставить небольшой промежуток.
4. Если отсутствуют единицы какого-либо разряда, вместо них пишут нули.
5. Если отсутствует целый класс, то вместо него пишут три нуля.

– Ребята, давайте вы попробуете сами записать многозначное число! – предложил Электроша. – Слушайте внимательно число: двадцать три миллиона пять тысяч двадцать три.
– Какие вы молодцы! – обрадовался за ребят Электроша. – Всё правильно написали!

А ещё вот что вам нужно знать, – продолжил он. – Запись натуральных чисел, которой мы пользуемся, называют десятичной. Такое название связано с тем, что 10 – это основа десятичной нумерации. Самое главное для вас сейчас – это понять, что десять единиц одного разряда образуют одну единицу следующего за ним разряда. Например, 10 единиц составляют 1 десяток, в свою очередь, 10 десятков – 1 сотню и так далее.
Числа 10, 100, 1000 и так далее называют разрядными единицами.

Зная это, вы сможете любое натуральное число представить в виде суммы разрядных слагаемых. К примеру, возьмём число 8 543. Его можно записать суммой разрядных слагаемых так:
8 543 = 8 000 + 500 + 40 + 3.
Или вот так: 8 543 = 8 · 1 000 + 5 · 100 + 4 · 10 + 3.
Последнее равенство называют записью числа 8 543 в виде суммы разрядных слагаемых.

– А теперь, ребята, давайте посмотрим, как вы всё поняли и выполним несколько заданий.
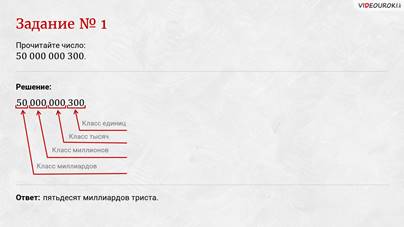
Задание первое: прочитайте число 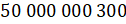 .
.
Решение: мысленно делим наше число на группы по три цифры начиная справа. Три первых цифры составляют класс единиц, три следующих – класс тысяч, ещё три следом – класс миллионов и последние – класс миллиардов. Видим, что в классе миллионов и классе тысяч стоят нули, значит, в этих классах отсутствуют единицы в разрядах. Тогда указанное число – пятьдесят миллиардов триста.
Следующее задание: запишите цифрами число пять миллионов одиннадцать тысяч шестьсот один.
Решение: число пишем слева направо. Старший класс в нашем числе – миллионы, и их пять, значит, записываем цифру 5. Следующий класс – тысячи. Сказано, что в числе их одиннадцать, значит, отсутствует разряд сотен и вместо него мы запишем цифру 0. За ней ставим 11. И последний класс в этом числе – класс единиц, их 601, разряд десятков отсутствует, на его месте ставим цифру 0.

И последнее задание: запишите число 7 506 в виде суммы разрядных слагаемых.
Решение: у нас в числе семь тысяч, значит, пишем 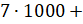 … дальше идёт класс единиц… пишем
… дальше идёт класс единиц… пишем 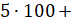 … видим в числе отсутствует разряд десятков, там стоит 0… значит, дальше пишем
… видим в числе отсутствует разряд десятков, там стоит 0… значит, дальше пишем 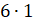 .
.
