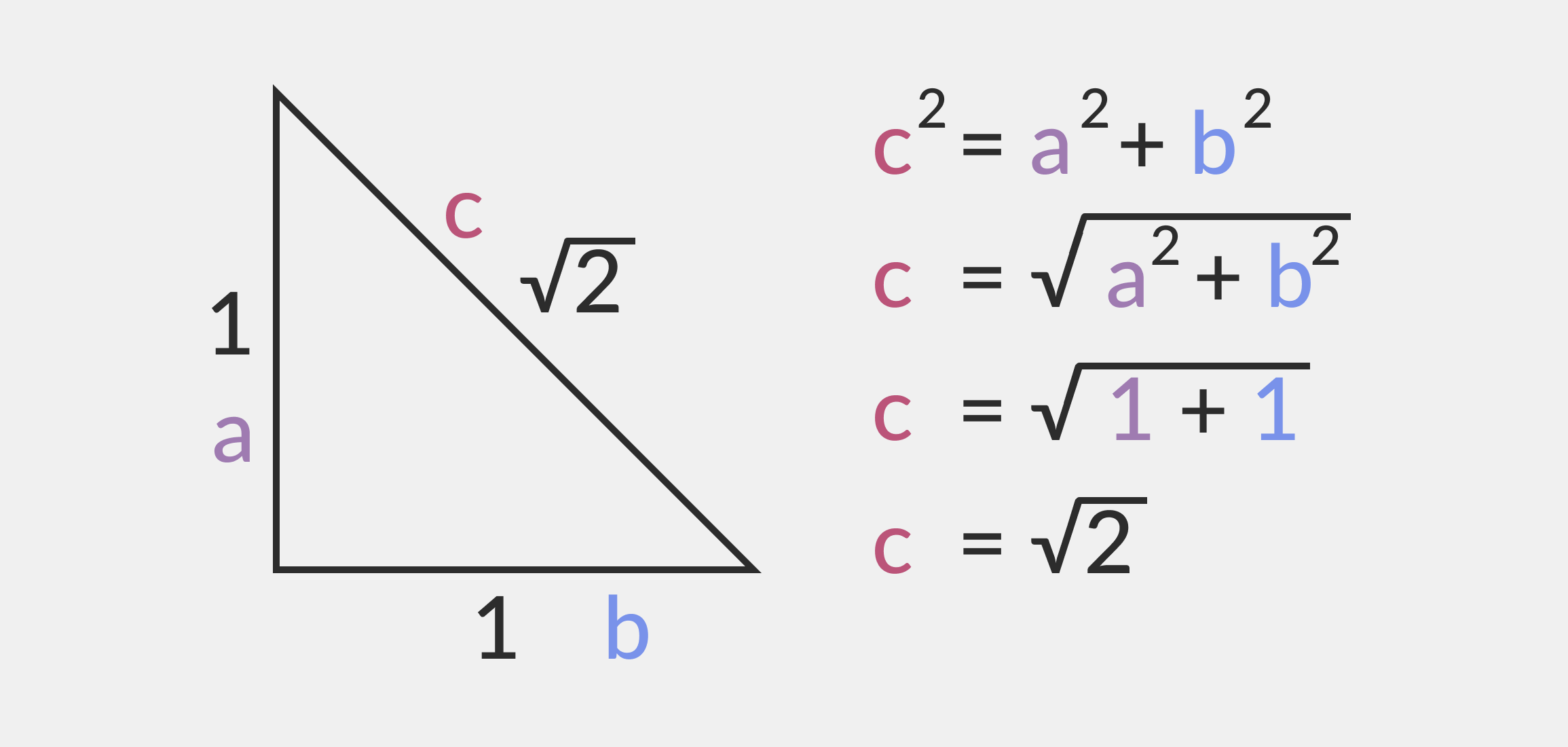Иррациональное число — это число, которое невозможно представить в виде дроби m/n, где m — целое число, а n — натуральное. Это определение довольно сухое и формальное — сейчас объясним понятнее.
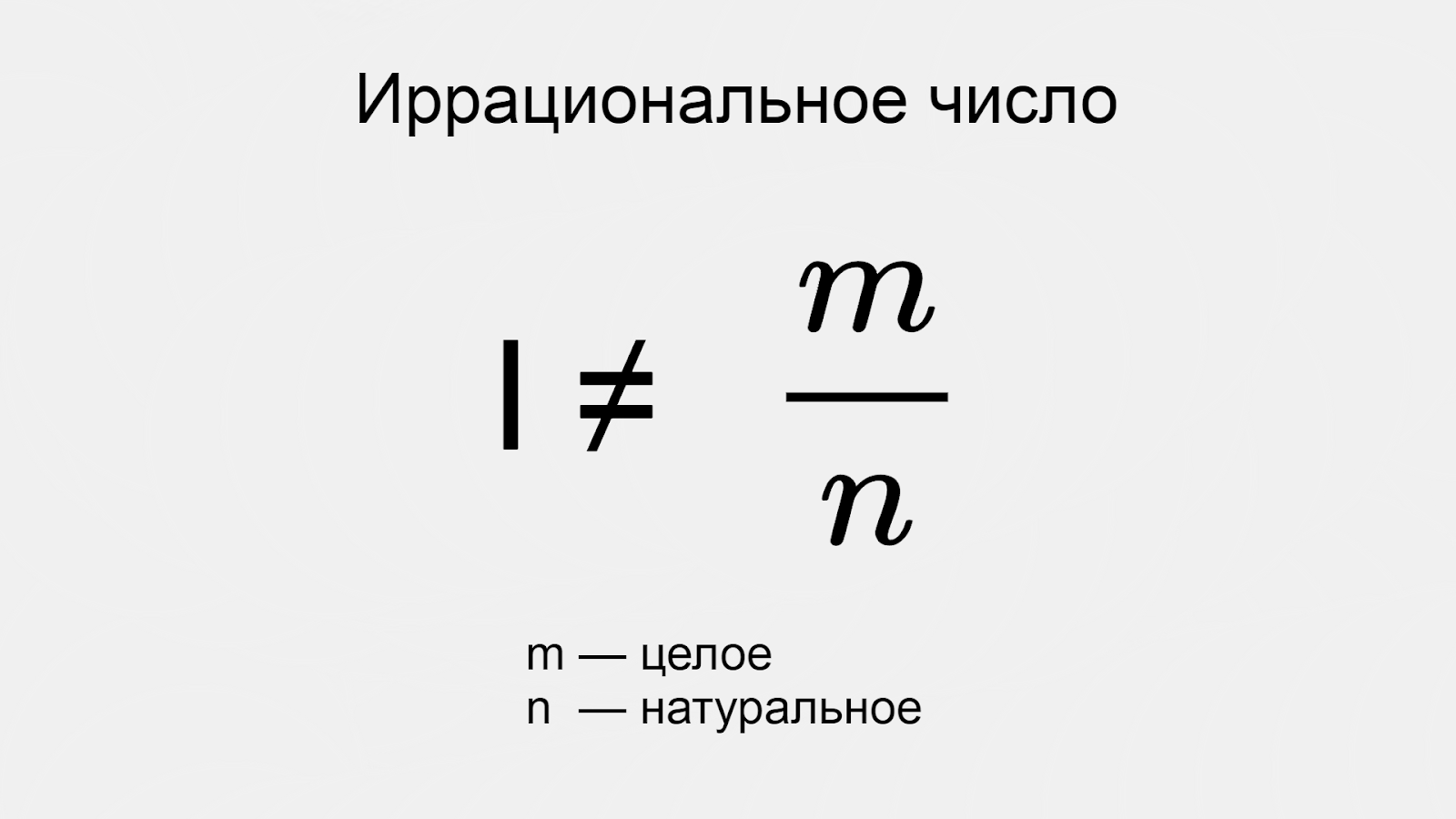
Простыми словами, иррациональное число — это бесконечная непериодическая дробь. «Бесконечная» означает, что у дроби есть бесконечное количество цифр после запятой. «Непериодическая» — что у этих цифр нет никакой повторяющейся закономерности.
Например, число √2 — иррациональное. Если попробовать извлечь из него корень с помощью калькулятора, получится число 1,4142135623… Цифры после запятой будут высчитываться бесконечно, а в их последовательности не будет никакой логики.
Другие примеры иррациональных чисел:
- Число Пи: π = 3,1415926535…
- Число Эйлера: e = 2,7182818284…
- Золотое сечение: φ = 1,6180339887…
- √2 = 1,4142135623…
- √3 = 1,7320508075…
- √5 = 2,2360679774…
- √7 = 2,6457513110…
- √11 = 3,3166247903…
Чем иррациональные числа отличаются от рациональных
Рациональные числа — это числа, которые можно представить в виде обыкновенной дроби — то есть деления двух целых чисел. Например, 0,5 можно записать как 5/10, а 6 — как 6/1.
Если в этих дробях разделить числитель на знаменатель, у нас получится ясный и предсказуемый результат — либо целое число, либо десятичная дробь. В крайнем случае, на выходе будет бесконечная периодическая дробь — такая, где есть повторяющееся значение после запятой.
Иррациональные числа устроены по-другому. Как бы вы ни старались, оно всегда будет принимать форму бесконечной непериодической дроби. Что-то вроде уже знакомого нам числа Пи: 3,1415926535… Поэтому их нельзя представить в виде дроби — просто нет двух чисел, которые при делении давали бы такого монстра
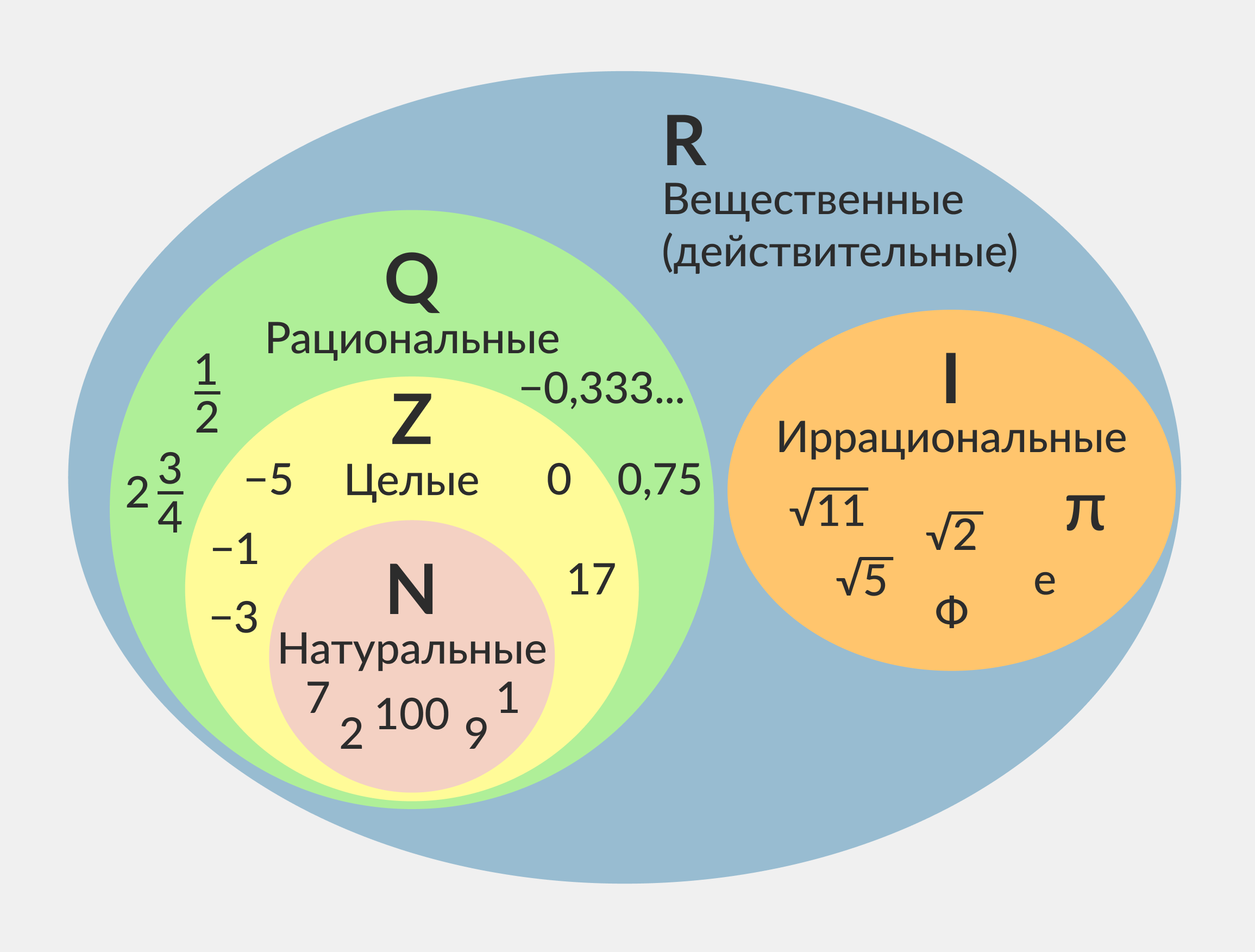
А вообще, оба вида чисел — иррациональные и рациональные — вместе образуют множество вещественных чисел. Это все числа, которые мы используем при повседневных расчётах. За пределами этого «пузыря» есть и другие числа — например, мнимые, но это уже тема для отдельной статьи.
Свойства иррациональных чисел
У иррациональных чисел, как и у любых других, есть свои свойства. Давайте пройдёмся по каждому из них.
1. Если сложить иррациональное число с рациональным, получится иррациональное число:
π + 2 = 3,1415926535… + 2 = 5,1415926535…
√2 + 3 = 1,4142135623… + 3 = 4,4142135623…
Это же правило действует и при вычитании:
π − 3 = 3,1415926535… − 3 = 0,1415926535…
√7 − 1,645 = 2,6457513110… − 1,645 = 1,0007513110…
2. Если умножить иррациональное число на рациональное, получится иррациональное число:
π ∙ 8 = 3,1415926535… ∙ 8 = 25,1327412287…
√5 ∙ 3 = 2,2360679774… ∙ 3 = 6,7082039324…
3. Если вычесть одно иррациональное число из другого, может получиться рациональное или иррациональное число:
π − π = 3,1415926535… − 3,1415926535… = 0
√3 − √2 = 1,732050807… − 1,4142135623… = 0,3178372451…
4. При сложении или умножении двух иррациональных чисел может получиться рациональное или иррациональное число:
π + π = 3,1415926535… + 3,1415926535… = 6,2831853071… = 2π
√3 ∙ √27 = √81 = 9
Иррациональные числа в геометрии
Иррациональное значение можно встретить, вычисляя длину гипотенузы единичного равностороннего треугольника. Это такой треугольник, где оба катета равны единице. Если мы попробуем вычислить гипотенузу такого треугольника, то получим иррациональное число — √2.