На одном из прошлых уроков мы с вами говорили о том, что любое механическое состояние тела (или системы тел) определяется его положением относительно других тел (то есть координатами) и его скоростью. И если изменяется хотя бы одна из этих величин, то говорят об изменении механического состояния тела или системы тел. Количественно механическое состояние системы и её изменение характеризуется механической энергией.
Таким образом, механическая энергия — это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу. При этом следует помнить, что энергия системы в данном состоянии не зависит от пути перехода её в это состояние.
Теперь давайте с вами вспомним, как энергия тела зависит от его скорости. Итак, пусть у нас есть тело массы т, которое совершает перемещение под действием постоянной силы (это может быть одна сила или равнодействующая нескольких сил), направленной вдоль перемещения.
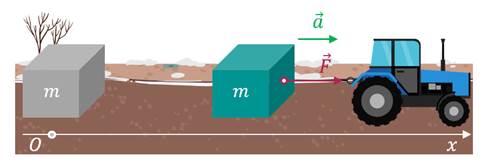
Выберем координатную ось Оx так, чтобы её положительное направление совпадало с направлением перемещения тела. Теперь вспомним, что согласно второму закону Ньютона единственным результатом действия этой силы будет сообщение материальной точке ускорения:
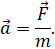
Кроме того, как мы уже знаем, она будет совершать работу:
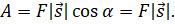
Сразу же учтём, что в выбранной системе координат 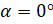 . Тогда
. Тогда 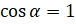 .
.
Так как тело движется с ускорением, то модуль его перемещение при переходе из начального положения в конечное можно найти по известной кинематической формуле:
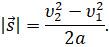
Теперь подставим выражения для силы и модуля перемещения тела в формулу для работы:
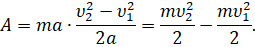
После несложных преобразований получим формулу, связывающую работу равнодействующей силы с изменением величины 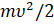 .
.
Ещё в седьмом классе вам говорили о том, что физическая величина, равная половине произведения массы тела на квадрат его скорости называется кинетической энергией. И ею обладают любые движущиеся тела.
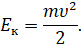
А единицей измерения кинетической энергии в СИ является джоуль:
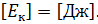
Как видно из формулы, кинетическая энергия тела — величина скалярная, которая зависит от модуля скорости тела, но не зависит от её направления.
Давайте перепишем уравнение для работы силы с учётом введённых обозначений:
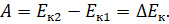
Полученная нами формула выражает математическую запись теоремы об изменении кинетической энергии: изменение кинетической энергии тела при его перемещении равно работе равнодействующей всех сил, действующих на него. Эта теорема справедлива для любых сил, действующих на тело.
Из теоремы следует, что когда результирующая сила действует по направлению движения тела и, следовательно, совершает положительную работу, то кинетическая энергия тела увеличивается. Если же результирующая сила направлена в сторону, противоположную движению, она совершает отрицательную работу, и кинетическая энергия тела уменьшается. А когда работа результирующей силы равна нулю кинетическая энергия тела остаётся неизменной.
Здесь также необходимо отметить, что поскольку скорость тела зависит от выбора инерциальной системы отсчёта, то и кинетическая энергия также зависит от выбора системы отсчёта.

Так например, для байкера, сидящего неподвижно относительно мотоцикла, она равна нулю в системе отсчёта, связанной с мотоциклом, и отлична от нуля, в системе отсчёта, связанной с Землёй.
Второй вид энергии, с которым вы знакомились в 7 классе), — это потенциальная энергия. Давайте сразу вспомним, что потенциальная энергия — это энергия системы, определяемая взаимным расположением тел (или частей тела друг относительно друга) и характером сил взаимодействия между ними.
В механике принято выделять два вида потенциальной энергии — это потенциальная энергия тела в гравитационном поле Земли и потенциальная энергия упруго деформированного тела. Мы с вами пока будем рассматривать только потенциальную энергию тела в поле тяготения.
Итак, потенциальная энергия тела в поле тяготения — это энергия, обусловленная взаимодействием тела с Землёй. Она зависит от их взаимного положения и равна работе, которую совершает сила тяжести при перемещении тела из данного положения на нулевой уровень.:
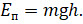
Измеряется потенциальная энергия в тех же единицах, что и работа:
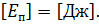
Так как нулевой уровень мы можем выбирать абсолютно произвольно, то потенциальная энергия в поле тяготения определяется неоднозначно. Однако физический смысл имеет только разность потенциальных энергий. А эта разность не зависит от выбора нулевого уровня.
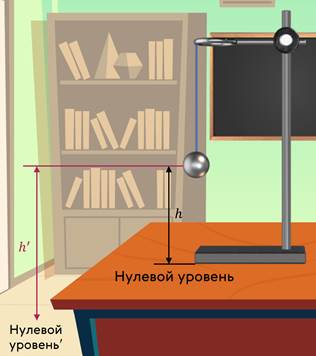
Рассмотрим ещё одно свойство потенциальной энергии. Предположим, что тело известной массы падает с высоты h1 до высоты h2. Очевидно, что в этом случае работу совершает сила тяжести. Причём эта работа будет положительной:
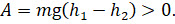
А вот изменение потенциальной энергии тела будет меньше нуля:
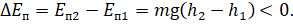
Сравнивая два выражения мы можем сказать, что работа силы тяжести равна убыли потенциальной энергии тела в гравитационном поле Земли.
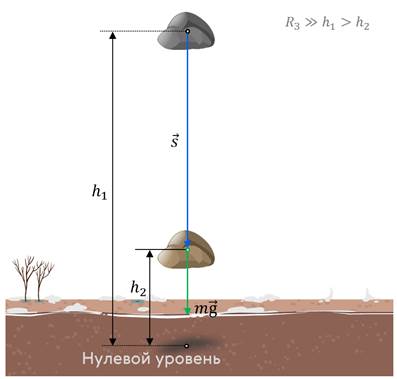
Конечно же любое тело может обладать двумя видами механической энергии одновременно. Но вот вопрос, могут ли измениться и кинетическая и потенциальная энергии одновременно?
Давайте с вами рассмотрим простую систему тел, состоящую из Земли и мяча. Будем считать, что мяч свободно падает и на некоторой высоте h1 его скорость равнялась υ1. А на высоте h2— увеличилась до υ2. Так как мяч находится в свободном падении, то на него действует только сила тяжести со стороны Земли, которая будет совершать работу по его перемещению с одного уровня на другой. С одной стороны, эта работа равна изменению потенциальной энергии мяча, взятой с обратным знаком:
𝐴 = –ΔЕп.
А с другой стороны (так как меняется скорость мяча), эту же работу можно найти на основании теоремы об изменении кинетической энергии:
𝐴 = ΔЕк.
Обратим внимание на то, что работу силу тяжести, действующую на Землю со стороны камня, мы не учитываем, так как она практически равна нулю из-за огромной массы нашей планеты.
Таким образом мы с вами получаем два уравнения для нахождения одной и той же физической величины — работы силы тяжести. Поэтому мы можем приравнять их правые части:
–ΔEп = ΔEк
Из полученного равенства видно, при свободном падении мяча его потенциальная энергия уменьшалась ровно на столько, на сколько увеличивалась энергия кинетическая. Отсюда следует, что изменение суммы кинетической и потенциальной энергий равно нулю:
Δ(Eп + Eк) = 0.
Сумма кинетической и потенциальной энергий тел, входящих в систему, называется полной механической энергией системы:
Е = Eп + Eк = const.
Такой же результат мы получим и при действии силы упругости.
Таким образом, полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остаётся неизменной. Это утверждение называется законом сохранения энергии в механике.
Обратите внимание на то, что сохраняются не кинетическая и потенциальная энергия по отдельности, а их сумма.
А теперь давайте с вами проведём простой опыт. Придадим начальную скорость деревянному бруску, находящемуся на поверхности стола.
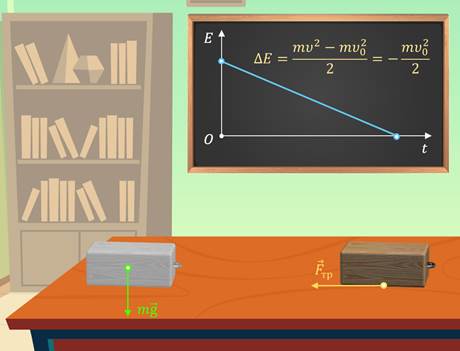
Пройдя некоторое расстояние, брусок остановится из-за действия силы трения — внутренней силы системы «брусок — стол». Несмотря на то что внешняя сила (сила тяжести) работу не совершала, механическая энергия этой системы уменьшилась на величину 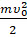 .
.
Таким образом, если в замкнутой системе между телами действует сила трения, то полная механическая энергия убывает. Причём изменение механической энергии равно работе силы трения:
ΔE = Атр.
Не сохраняется полная механическая энергия и в том случае, если в системе тел происходят неупругие деформации.
Но убывание механической энергии не означает, что энергия бесследно исчезла. Так, в нашем примере, при движении бруска по столу происходило нагревание бруска и стола. Только оно было мало́, а потому незаметно.
Нагревание происходит и при неупругих деформациях. Согните и разогните несколько раз подряд металлическую проволоку. Вы почувствуете, что в месте сгиба она нагрелась.
Что общего у этих явлений? То, что действие сил трения и сопротивления приводит к увеличению внутренней энергии тел.
Весь накопленный опыт и специально проведённые эксперименты показывают, что в любой замкнутой системе уменьшение механической энергии в точности равно увеличению внутренней.
Таким образом, для любой замкнутой системы тел ВСЕГДА выполняется закон сохранения и превращения энергии: величина полной энергии замкнутой системы остаётся неизменной. При этом, будучи не созидаемой и неуничтожаемой, энергия может превращаться из одного вида в другой.
Закон сохранения и превращения энергии является одним из важнейших законов не только физики, но и всех других наук о природе.