В этом уроке мы не будем разбирать, как решаются линейные или квадратные неравенства. Нас будет интересовать только вопрос: «Как записать ответ неравенства специальными математическими знаками,
например, в виде x ∈ (3; +∞) ?».
Стоит отметить, что далеко не во всех учебных заведениях требуют обязательно записывать ответ неравенства в виде x ∈ (3; +∞) . В некоторых школах в 8 и 9 классе разрешают оставлять ответ, используя знаки
больше «>» и «<». Например, следующим образом.
Впрочем, мы рекомендуем освоить запись ответа неравенства в математических обозначениях сразу, так как в любом случае в старшей школе и затем в университете будут требовать именно такую запись ответа.
Перед разбором, как записывать ответ неравенства математическими знаками, вспомним расшифровку и обозначение этих знаков.
| ∈ |
«Принадлежит» Легко запомнить знак, как зеркальное отображение русской буквы «Э» или как символ евро «€», но только с одной палочкой посередине. |
|
| ( … ) | «Круглые скобки» Используются, когда число на границе интервала НЕ входит в сам интервал. На числовой оси такие числа обозначают «пустой» точкой. |
|
| [ … ] | «Квадратные скобки» Используются, когда число на границе интервала входит в сам интервал. На числовой оси такие числа обозначают «заполненной» точкой. |
|
| ∪ | «Объединение» Знак похож на подковку. Используется для объединения двух и более интервалов. |
|
| + ∞ | «Плюс бесконечность» Изображается как цифра «8» на боку со знаком «+» слева. Обозначает бесконечность на положительном (правом) краю числовой оси. |
|
| − ∞ | «Минус бесконечность» Изображается как цифра «8» на боку со знаком «−» слева. Обозначает бесконечность на отрицательном (левом) краю числовой оси. |
|
Перейдем к непосредственной записи ответа неравенства. Рассмотрим и решим линейное неравенство.
x > 6 + 8
x > 14
Мы решили линейное неравенство, теперь запишем его ответ с помощью математических знаков.
 Перед тем, как записывать ответ неравенства, обязательно изобразите его на числовой оси.
Перед тем, как записывать ответ неравенства, обязательно изобразите его на числовой оси.
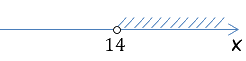
Итак, мы изобразили ответ неравенства на числовой оси. После этого запишем слово «Ответ:» и за ним запишем «x ∈». Такая запись читается как «икс принадлежит».
Взглянув на рисунок ответа на числовой оси, мы видим, что область решений начинается с числа «14». Число «14» не входит в область решений («пустая» точка на оси). Значит, используем круглую скобку.
Нам остается понять, где заканчивается область решений справа. Правильный ответ — справа область заканчивается в положительной бесконечности «+ ∞».

На числовой оси на обоях краях слева и справа соответственно расположены «минус» и «плюс» бесконечности. Как правило, их не рисуют на числовой оси лишний раз, т.к. их наличие на оси подразумевается.
Запишем окончательный ответ.
Знаки «+ ∞» и «− ∞» всегда записываются с круглыми скобками.
Разберем другой пример.
−7x ≥ 56 | :(−7)
x ≤ 8
Также как и в предыдущем примере всегда начинаем записывать
ответ с записи «x ∈…».

В ответе «x ≤ 8» область решений начинается с «− ∞» и заканчивается на «8», которое входит в ответ. Значит, «8» будет с квадратной скобкой. Так и запишем в ответе.
Запись ответа неравенства для квадратных неравенств
При решении квадратных неравенств часто может получаться несколько интервалов в ответе. Разберемся, как их записывать в ответ. Рассмотрим пример квадратного неравенства и его решение.
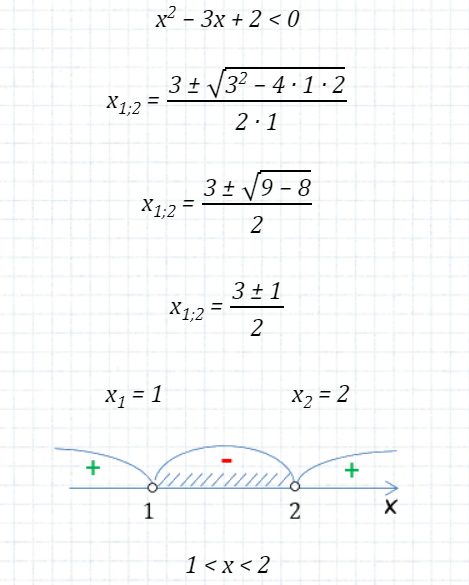
В ответе мы получили один интервал. Запишем его в ответ. Как обычно, начнем запись ответа с «x ∈». Далее используем круглые скобки, т.к. оба числа не входят в границы интервалов.
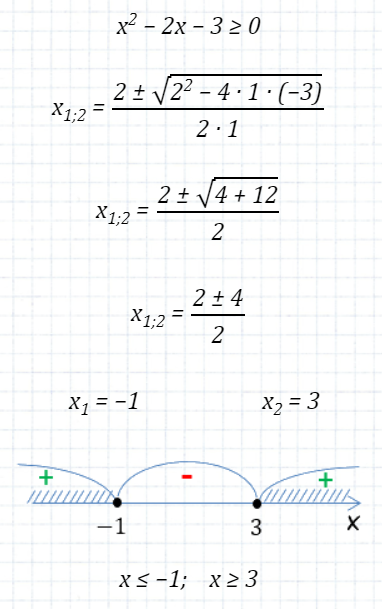
В ответе неравенства мы получили два интервала в области решений
(x ≤ −1; x ≥ 3) и оба интервала нужно записать в ответ. Запись ответа неравенства всегда делается слева направо (как мы привыкли читать).
Начнем слева направо записывать интервалы в ответ. Первый интервал начинается с «минус» бесконечности и заканчивается на «−1» (включительно). Так и запишем.
Второй интервал начинается с «2»(включительно) и заканчивается на «плюс» бесконечности. Для объединения интервалов используем знак «∪» («объединение»).