При равномерном движении по кривой вектор скорости, оставаясь постоянным по величине, изменяется по направлению. Изменение скорости однозначно связано с ускорением. Представим себе равномерное движение по окружности. Изменение скорости направлено к центру. Направление вектора ускорения совпадает с направлением вектора изменения скорости. Следовательно, при равномерном движении точки по окружности она имеет ускорение, направленное к центру этой окружности. Оно так и называется: центростремительное ускорение. Обычно обозначается латинской буквой «a» с добавлением двух русских букв «цс».
Формулы для решения:
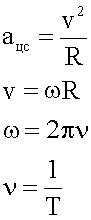
В этих формулах «v» — скорость равномерного движения по окружности, «омега» — угловая скорость этого движения, «ню» — частота, «T» — период вращения.
Алгоритм решения типовой задачи:
1. Кратко записать условие задачи.
2. Изобразить графически движение, нарисовав окружность вращения и обозначив стрелками скорость и центростремительное ускорение.
3. Ввести систему отсчета, введя начало отсчета времени и выбрав оси координат для движения и скорости. Часто бывает удобно разместить начало системы координат на движущейся точке, направив одну ось вдоль радиуса, куда направлено и центростремительное ускорение, тогда вторая ось будет направлена вдоль скорости по касательной к окружности.
4. Записать необходимые для решения формулы из числа вышеуказанных. Составить из них уравнение или систему уравнений, с помощью которых можно найти неизвестную величину.
5. Решить уравнение или систему в общем виде.
6. Подставить заданные величины в общее решение, вычислить.
7. Записать ответ.
Возможные особенности задач:
Почти во всех задачах не учитывается круговое движение тела, совершаемое им вместе с Землей. Однако, существуют задачи, где рассматривается движение именно Земли. В этом случае, не учитывается ее движение в составе Солнечной системы. В общем случае, при решении принимается в расчет только тот уровень движения, о котором говорится в задаче.
Примеры решения:
Задача 1.
Определите с какой скоростью и ускорением движутся точки земной поверхности на экваторе? При решении учитывать только вращение Земли вокруг своей оси. Радиус Земли 6400 км.
Решение.
1. Кратко записываем условие задачи.
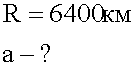

2. Изображаем графически движение, нарисовав окружность вращения точек экватора Земли вокруг ее оси и обозначив стрелками скорость и центростремительное ускорение. Ввиду того, что скорость вращения Земли постоянна, другого ускорения, кроме центростремительного нет.
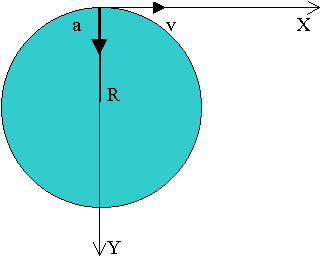
3. Вводим систему отсчета. Удобнее всего разместить начало системы координат на одной из точек поверхности Земли, направив одну ось вдоль радиуса, куда направлено и центростремительное ускорение, тогда вторая ось будет направлена вдоль скорости вращения по касательной к окружности.
4. Записываем необходимые для решения формулы. Надо учесть, что в задаче неявно задан период вращения — это 1 сутки.
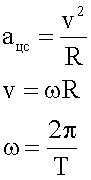
5. Решаем систему в общем виде.
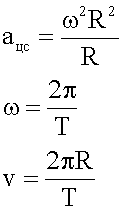
Отсюда имеем простое выражение для «a»: ![]()
куда подставляем выражение для «омега» 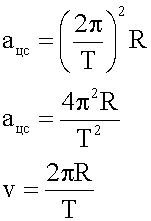
6. Подставляем заданные величины в общее решение, вычисляем. Перед подстановкой переводим в одну систему единиц — в СИ.
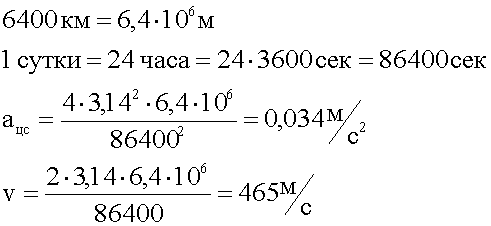
7. Записываем ответ.
Ответ: Скорость точек поверхности Земли на экваторе 465 м/с, центростремительное ускорение 0,034 м/с за секунду.
Задача 2.
Поезд проходит закругление рельсового пути радиусом 300 метров с постоянной скоростью 20 км/час. Какое ускорение испытывают пассажиры?
Решение.
1. Кратко записываем условие задачи.
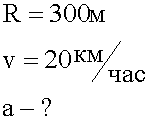
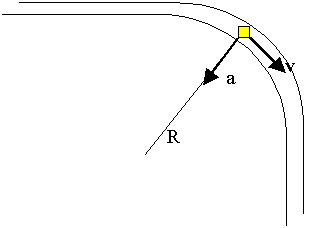
2. Изображаем графически движение, нарисовав закругление пути как часть окружности и обозначив стрелками скорость и центростремительное ускорение. Скорость по величине не меняется, поэтому все ускорение сводится к центростремительному.
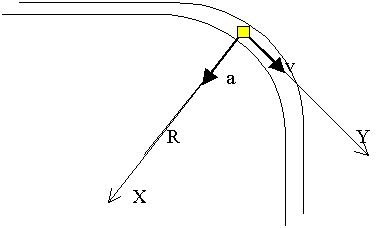
3. Вводим систему отсчета, разместив начало системы координат на движущемся поезде, который в заданных условиях мы считаем точкой. Одну ось направляем вдоль радиуса, куда направлено и центростремительное ускорение, тогда вторая ось будет направлена вдоль скорости по касательной к окружности закругления.
4. Записываем формулы для решения. Нужна всего одна. 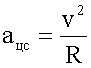
5. Решение в общем виде дает сама формула.
6. Подставляем заданные величины в общее решение, вычисляем. Перед подстановкой переводим в единую систему единиц — СИ.
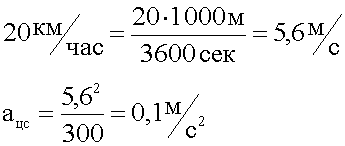
7. Записываем ответ.
Ответ: Пассажиры поезда испытывают центростремительное ускорение 0,1 м/с за секунду.
Задача 3.
Каков радиус поворота конькобежца, если он поворачивает со скоростью 3 м/сек и испытывает при этом ускорение 5 м/сек за секунду.
Решение.
1. Кратко записываем условие задачи.
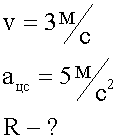

2. Изображаем графически движение, нарисовав траекторию поворота конькобежца как часть окружности и обозначив стрелками скорость и центростремительное ускорение.
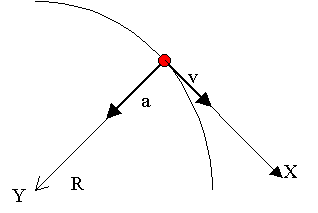
3. Вводим систему отсчета, разместив начало системы координат на конькобежце, которого считаем движущейся точкой и направив одну ось вдоль радиуса, куда направлено и центростремительное ускорение. Тогда вторая ось будет направлена вдоль скорости по касательной к окружности.
4. Записываем необходимые для решения формулы. В данном случае формула одна. 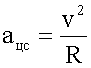
5. Решаем уравнение в общем виде.

6. Подставляем заданные величины в общее решение, вычисляем.
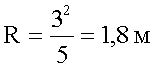
7. Записываем ответ.
Ответ: радиус поворота конькобежца 1,8 м.
Равномерное движение по окружности. Центростремительное ускорение.
Задача.
Мальчик вращает камень, привязанный к веревке длиной 0,5 м в вертикальной плоскости. Веревка обрывается в тот момент, когда скорость направлена вертикально вверх и камень взлетает на высоту 4,5 м. Сколько оборотов в секунду делал камень к моменту отрыва?
Решение.
1. Краткая запись условия.
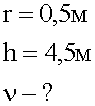
2. Графическая запись условия.

3. Решение в общем виде.
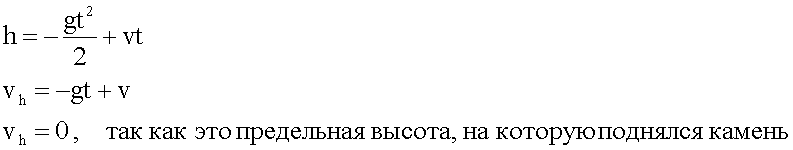
Отсюда получаем:
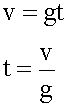
Подставляем выражение для времени в формулу для высоты.

Отсюда находим скорость момент отрыва.
![]()
Это линейная скорость вращавшегося камня. Зная ее и радиус вращения находим:

4. Подстановка значений, вычисление.
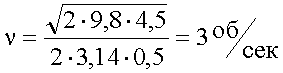
5. Запись ответа.
Ответ: Мальчик вращал камень с частотой 3 оборота в секунду.
Задача.
Какое движение совершают ролики подшипника во время его работы?
Решение.
Ролики подшипника совершают довольно сложное движение: они вращаются вокруг своей оси и, кроме того, их оси вращаются вокруг общего центра — оси подшипника.
Задача.
Центростремительное ускорение вращения тела в результате уменьшения частоты вращения в 3 раз, стало 0,5 м/с2 . Чему было равно центростремительное ускорение вначале?
Решение.
1. Краткая запись условия.
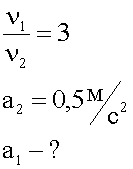
2. Графическая запись условия.
Рисунок ввиду простоты задачи может быть мысленный.
3. Решение в общем виде.

Записываем полученное выражение для ускорения в первом и во втором случаях.
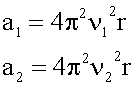
Делим первое уравнение на второе.
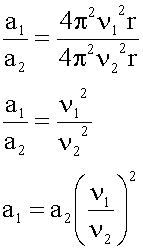
4. Подстановка значений, вычисление.
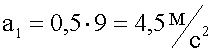
5. Запись ответа.
Ответ: Начальное центростремительное ускорение было 4,5 м/с за секунду.
Независимость движений. Сумма равномерного и равноускоренного движений. Движение тела под углом к горизонту.
Задача.
Пуля вылетает из горизонтально расположенного ружья со скоростью 700 м/с. На сколько снизится пуля в вертикальном направлении за время полета, если цель находится на расстоянии 500 м. (g=9,8 м/с2 )
Решение.
1. Краткая запись условия.
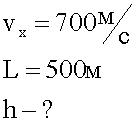
2. Графическая запись условия.

3. Решение в общем виде.
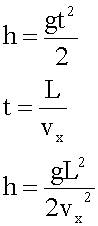
4. Подстановка значений, вычисление.
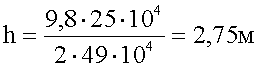
5. Запись ответа.
Ответ: За время полета на 500 метров пуля снизится на 2,75 метра.
Задача.
Пуля вылетает из горизонтально расположенного ружья со скоростью 300 м/с. На каком расстоянии от места выстрела упадет пуля, если высота ружья над поверхностью земли равна 1,25 м.
Решение.
1. Краткая запись условия.

2. Графическая запись условия.

3. Решение в общем виде.
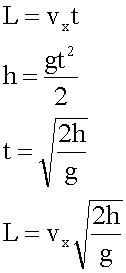
4. Подстановка значений, вычисление.
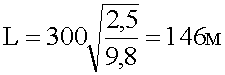
5. Запись ответа.
Ответ: Пуля упадет на землю на расстоянии 146 метров от ружья.
Задача.
Дальность полета тела в два раза больше высоты его подъема. Под каким углом к горизонту брошено тело?
Решение.
1. Краткая запись условия.
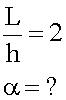
2. Графическая запись условия.
Рисунок делаем мысленный в силу простоты условия.
3. Решение в общем виде.
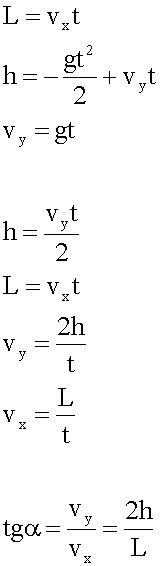
4. Подстановка значений, вычисление.
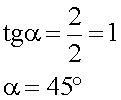
5. Запись ответа.
Ответ: Тело бросили под углом 45 градусов.
Задача.
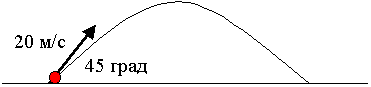
Мяч брошен под углом 45′ к горизонту со скоростью 20 м/с. На каком расстоянии он упадет на землю? какой наибольшей высоты достигнет при полете?
Решение.
1. Краткая запись условия.
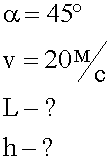
2. Графическая запись условия.
3. Решение в общем виде.
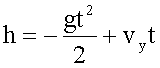
За время максимального подъема мяч пролетит половину горизонтального расстояния. Поэтому:
![]()
Находим горизонтальную и вертикальную проекции скорости.
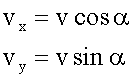
Учитываем, что
![]()
Подставляя в уравнения движения, получаем:
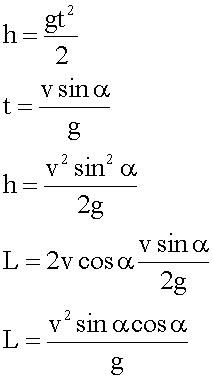
4. Подстановка значений, вычисление.
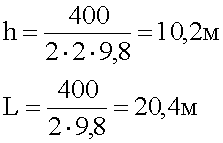
5. Запись ответа.
Ответ: Мяч пролетит 20,4 метра, достигнув наибольшей высоты 10,2 метра.
Задача.
Как будет изменяться ускорение, с которым движется груз по наклонной плоскости при увеличении у нее наклона?
Решение.
1. Краткая запись условия.
2. Графическая запись условия.

3. Решение в общем виде.
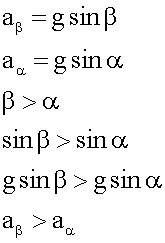
4. Запись ответа.
Ответ: С увеличением угла ускорение увеличивается.
Задача.
Какие из приведенных зависимостей описывают равнопеременное движение? а) V =3 +2t; б) S =3+2t; в) S=3t2; г) S=3t- t2; д) S=2 — 3t+4t2
Решение.
1. Краткая запись условия.
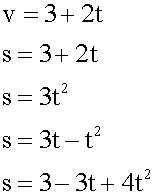
2. Графическая запись условия.
Мысленный рисунок
3. Решение в общем виде.
Для равнопеременного движения характерна квадратичная зависимость пути от времени и линейная зависимость скорости от времени. Исходя из этого, записываем ответ.
Ответ: а, в, г, д.
Задача.
С аэростата, находящегося на высоте 1 км, произведен вертикально вверх выстрел, причем пуля вылетела скоростью 200 м/с. Через сколько времени пуля упадет на Землю?
Решение.
1. Краткая запись условия.
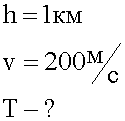
2. Графическая запись условия.
3. Решение в общем виде.
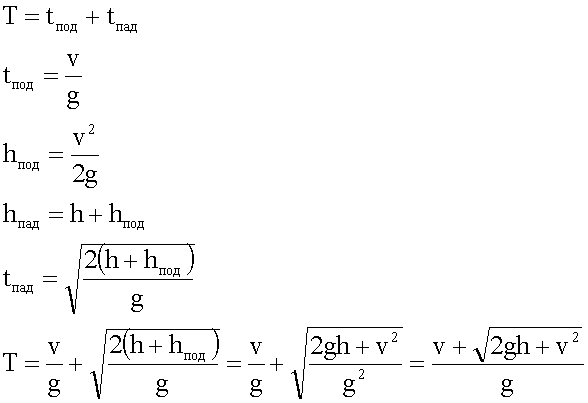
4. Подстановка значений, вычисление.
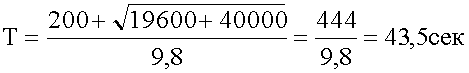
5. Запись ответа.
Ответ: Пуля упадет на землю через 43,5 секунды после выстрела.
Сложение векторов. Разложение векторов на составляющие. Независимость движений.
Задача.
Санки, скатываясь с горы, в некоторый момент времени имеют скорость 10 м/с. Чему равны горизонтальная и вертикальная составляющие скорости, если наклон горы составляет 30 градусов к горизонту? Чему должен равняться наклон горы, чтобы обе составляющие были равны?
Решение.
Краткая запись условия
По сути дела, здесь два условия. Первое:
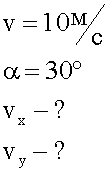
Второе:
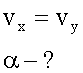
2. Графическая запись условия.

3. Решение в общем виде.
Для первого условия:
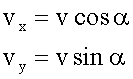
Для второго условия:

4. Подстановка значений, вычисление.
Для первого условия:
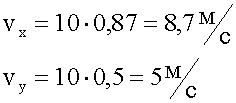
Для второго условия:
![]()
5. Запись ответа.
Ответ: Горизонтальная составляющая скорости 8,7 м/с, вертикальная составляющая скорости 5 м/с. Для того, чтобы вертикальная и горизонтальная составляющая скорости были равны угол наклонной плоскости должен быть равен 45 градусам.
Задача.
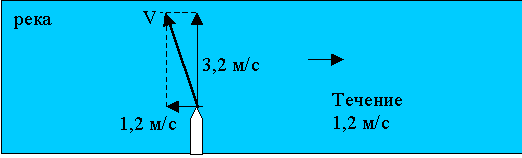
Какую скорость должен сообщить мотор катеру относительно воды, что бы при скорости течения реки 1,2 м/с, катер двигался перпендикулярно берегу со скоростью 3,2 м/с?
Решение.
1. Краткая запись условия.
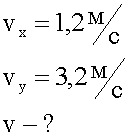
2. Графическая запись условия.
3. Решение в общем виде.
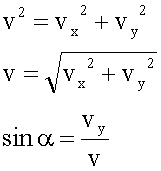
4. Подстановка значений, вычисление.
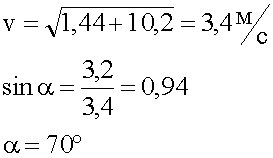
5. Запись ответа.
Ответ: Мотор должен сообщить катеру скорость 3,4 м/с, направленную под углом 70 градусов к перпендикулярному направлению движения.
Задача.
Самолет движется относительно воздуха со скоростью 50 м/с. Скорость ветра 15 м/с. Какова скорость самолета, если он движется: по ветру; против ветра; перпендикулярно направлению ветра?
Решение.
1. Краткая запись условия.
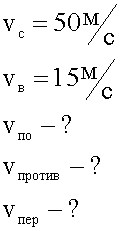
2. Графическая запись условия.
Рисунок можно сделать мысленно ввиду простоты.
3. Решение в общем виде.
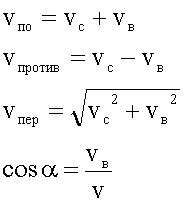
4. Подстановка значений, вычисление.

5. Запись ответа.
Ответ: Самолет движется по ветру со скоростью 65 м/с, против ветра — 35 м/с, перпендикулярно ветру — 53,5 м/с под углом 16 градусов к направлению собственной скорости.
Механическое движение. Равномерное прямолинейное движение. Средняя скорость. Относительность движения.
Задача.
Первую половину пути тело имело скорость 54 км/ч, а вторую половину — 25 м/с. Определить среднюю скорость на всем пути.
Решение.
1. Краткая запись условия.
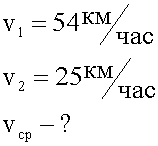
2. Графическая запись условия.
Рисунок делается мысленно ввиду простоты условия.
3. Решение в общем виде.
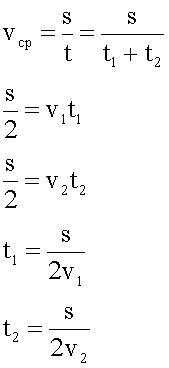
Подставляем выражения для времени в выражение для средней скорости
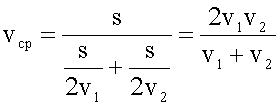
4. Подстановка значений, вычисление.
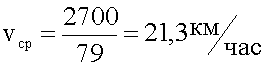
5. Запись ответа.
Ответ: Средняя скорость движения автомобиля 21,3 км/час.
Задача.
Автомобиль проехал первую половину пути со скоростью 20 км/ч, затем вернулся с той же скоростью назад. Определить среднюю скорость перемещения.
Решение.
1. Краткая запись условия.
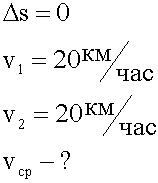
2. Графическая запись условия.
Рисунок делается мысленно ввиду простоты условия.
3. Решение в общем виде.
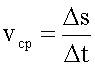
4. Подстановка значений, вычисление.
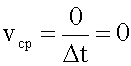
5. Запись ответа.
Ответ: Средняя скорость перемещения равна нулю.
Задача.
Два тела имеют скорости: v1= 5,4 км/ч,v2= 1,5 м/с. Скорость какого тела больше?
Решение.
1. Краткая запись условия.
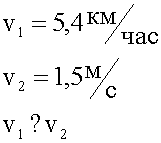
2. Графическая запись условия.
Рисунок делается мысленно ввиду простоты условия.
3. Решение в общем виде.
Надо перевести значения скорости в одни единицы.
4. Подстановка значений, вычисление.
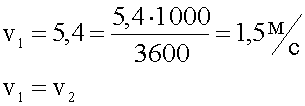
5. Запись ответа.
Ответ: Заданные скорости равны.
